آرایه در c++
تا اینجا با مسائلی روبرو بودیم که در آن نیاز به ذخیره حداکثر دو یا سه مقدار داشتیم، بنابراین به تعداد محدودی متغیر نیاز داشتیم. اما مساله ای را در نظر بگیرید که بخواهید 1000 عدد را ذخیره کنید. قطعا استفاده از 1000 متغیر ایده جالبی نیست. اینجاست که باید با مفهوم آرایه آشنا شوید. در ریاضیات، زمانی که متغیرها زیاد باشد از اندیس استفاده میکنند. مثلا x1 و x2 و … و xn؛ یعنی n متغیر.
در برنامه نویسی هم دقیقا از همین ایده استفاده میشود. فقط چون نمیتوانیم اندیس را مانند دستخط زیر متغیر بنویسیم و بر روی صفحه کلید، کلیدی برای این کار تعریف نشده است از [ ] استفاده میکنیم. یعنی x[1] و x[2] و …و x[n]. در مثال ساده زیر مفهوم آرایه را بیشتر توضیح میدیم:
مثال 1: برنامه ای بنویسید که 50 عدد از ورودی دریافت کند. ابتدا اعداد زوج و سپس اعداد فرد را چاپ کند
#include <iostream>
int main()
{
int A[50];
int i;
for(i=0;i<50;i++)
cin>>A[i];
for(i=0;i<50;i++)
if(A[i]%2 == 0)
cout<<A[i];
for(i=0;i<50;i++)
if(A[i]%2 == 1)
cout<<A[i];
return 0;
}توضیح کد:
خط 4: در این دستور آرایه A تعریف شده است. تفاوت تعریف آرایه و تعریف متغیر در مشخص کردن اندازه آرایه است. در این خط آرایه ای به طول 50 و از نوع int تعریف شده است.
خط 7 و 8: در این دو خط آرایه A از ورودی به این صورت دریافت میشود: به ازای i=0 وارد حلقه تکرار میشود و عددی که دریافت میشود در خانه صفر آرایه A (یا همان A[0]) ذخیره میشود سپس یک واحد به i اضافه میشود و اینبار عددی که از ورودی خوانده میشود در خانه یک آرایه (یا همان A[0]) ذخیره میشود و به همین ترتیب همه عناصر آرایه پر می شود.
نکته 1: خانه های آرایه از صفر شماره گذاری میشوند. بنابراین اگر یک آرایه 50 تایی داشته باشیم خانه های آن از صفر تا 49 شماره گذاری میشوند.
در خط 7 و 8 برنامه، اصطلاحا این گونه میگوییم: آرایه از ابتدا تا انتها پیمایش میشود و یکی یکی خانه های آرایه را میخواند. به همین صورت میتوانیم بگوییم که در خط 10 تا 12 آرایه از ابتدا تا انتها پیمایش میشود و اعداد زوج آرایه چاپ میشود و در ادامه و در خط 14 تا 16 آرایه از ابتدا تا انتها پیمایش میشود و اعداد فرد آرایه چاپ میشود.
مثال 2: برنامهای بنویسید که که ورودی یک آرایه را دریافت کند و واریانس اعداد آرایه را محاسبه کند
برای محاسبه واریانس اعداد X1 و X2 و … و Xn از فرمول زیر استفاده میکنیم:
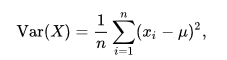
که
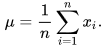
برای نوشتن این برنامه به سه پیمایش نیاز داریم. یکی برای دریافت آرایه، یکی برای محاسبه میانگین و دیگری برای محاسبه واریانس:
#include <iostream>
#include <cmath>
int main()
{
int const n=10;
int A[n];
int i;
cout<<"Enter Array A: ";
for(i=0; i<n ;i++)
cin>>A[i];
double sum=0;
for(int i = 0;i<n;i++)
sum += A[i];
double mu = sum/n;
sum = 0;
for(i=0 ; i<n;i++)
sum += pow((A[i] - mu),2);
cout<<sum/n;
return 0;
}توضیح کد:
خط 16 و 17: در این دو خط مجموع آرایه محاسبه شده است و در ادامه میانگین این اعداد در mu ذخیره شده. نکته قابل توجه در این مثال استفاده از عملگر =+ است. این عمگر به معنی این است که عبارت سمت راست را به متغیر سمت چپ اضافه کن. بنابراین در خط 17 مقدار A[i] به sum اضافه میشود.
خط 23 و 24: در این دو خط فرمول واریانس محاسبه میشود. در خط 24 از تابع pow یا همان تابع توان استفاده شده است که قبلا در مورد این تابع صحبت شده است. فقط یادآوری میکنیم که برای استفاده از این تابع باید فایل سرآیند cmath را به برنامه اضافه کنید.
در مثال 4 نحوه استفاده از const توضیح داده شده است.
مثال 3: برنامهای بنویسید که جملات اول تا 50ام دنباله فیبوناچی را در یک آرایه محاسبه کند.
#include <iostream>
int main()
{
int A[100];
int i;
A[0] = 1;
A[1] = 1;
for(i=2; i<50 ;i++)
A[i] = A[i-1] + A[i-2];
for(i=0;i<50;i++)
cout<<A[i]<<" ";
return 0;
}کد برنامه فیبوناچی بدون استفاده از آرایه را در ساختار تکرار بررسی کردیم. در آن مثال بدون استفاده از آرایه کدنویسی کردیم. همانطور که در این کد میبینید کدنویسی این سوال با آرایه ساده تر به نظر میرسد.
اگر این کد را اجرا کنید خواهید دید که ازاعداد 47 به بعد عدد منفی هم در لیست ظاهر میشود. برای دانستن علت این موضوع overflow را درگوگل سرچ کنید!
اگه دوست دارید میتونید آموزش کاملتری از آرایه رو در کانال تلگرامم ببینید:
مثال 4: برنامهای بنویسید که دو آرایه از ورودی دریافت کند و مجموع دو آرایه را چاپ کند.
#include <iostream>
int main()
{
int const n=10;
int A[n],B[n],C[n];
int i;
cout<<"Enter Array A:";
for(i=0; i<n ;i++)
cin>>A[i];
cout<<"Enter Array B:";
for(i=0; i<n ;i++)
cin>>B[i];
cout<<"sum of 2 Arrays:";
for(i=0; i<n ;i++)
C[i]=A[i] + B[i];
for(i=0; i<n ;i++)
cout<<C[i]<<" ";
return 0;
}توضیح کد:
در خط 5 برنامه از متغیر n و از جنس const استفاده شده است. این متغیر به چه معناست و چرا به آن نیاز داریم؟ در این مثال ما به چهار پیمایش آرایه نیاز داریم. و در همه این پیمایشها باید آرایه را تا خانه آخر پیمایش کنیم. اگر ما از متغیر n استفاده نمیکردیم باید به جای همه nها عدد 10 قرار میدادیم. حال فرض کنید تصمیم گرفتید که آرایهتان را به 100 خانه تغییر دهید. باید همه اعداد 10 در کدتان را به 100 تغییر دهید. علاوه بر اینکه دردسر این کار زیاد است، ممکن است یکی از ده ها را فراموش کنید به صد تغییر دهید و طبیعتا برنامه به درستی کار نمیکند. از طرف دیگر کامپایلر ++c شما را مجبور میکند که در حین تعریف آرایه اندازه آن را به صورت ثابت و const تعریف کنید. بنابراین باید متغیر n از نوع const تعریف شود.
مثال 5: برنامهای بنویسید که از 100 عدد دریافت کند و در آرایه قرار دهد. سپس بزرگترین عدد را چاپ کند.
این مثال در مبحث ساختار تکرار بدون استفاده از آرایه پیادهسازی شد. برای پیاده سازی با آرایه به دو پیمایش نیاز داریم: یکی برای خواندن آرایه و دیگری برای پیدا کردن ماکزیمم.
#include <iostream>
#include <cmath>
int main()
{
int const n=10;
int A[n];
int i;
cout<<"Enter Array A: ";
for(i=0; i<n ;i++)
cin>>A[i];
int max = A[0];
for(i=1;i<n;i++)
if(A[i]>max)
max = A[i];
cout<<max;
return 0;
}توضیح کد:
در خط 12 و 13 آرایه از ورودی دریافت میشود . در خط 15 فرض میکنیم عدد اول بزرگترین عدد است و در ساختار تکرار (خط 17 تا 19) از خانه دوم (i=2) تا خانه آخر یکی یکی خانه های آرایه را پیمایش میکنیم و تک تک خانهها را با max مقایسه میکنیم. چنانچه بزرگتر بود آن را در max ذخیره میکنیم.
در روش بالا بزرگترین خانه آرایه چاپ میشود، اما فرض کنید علاوه بر بزرگترین عدد به اندیس خانه بزرگترین عدد هم نیاز داشته باشیم. یعنی مثلا در انتها مشخص شود که عدد 158 که در خانه 7ام وجود دارد بزرگترین عدد آرایه است. برای این مساله کد زیر را پیاده سازی میکنیم:
#include <iostream>
#include <cmath>
int main()
{
int const n=5;
int A[n];
int i;
cout<<"Enter Array A: ";
for(i=0; i<n ;i++)
cin>>A[i];
int idx = 0;
for(i=1;i<n;i++)
if(A[i]>A[idx])
idx = i;
cout<<A[idx];
return 0;
}توضیح کد:
تفاوت این روش با روش قبل در استفاده از متغیر idx به جای max است. در مثال قبل در max بزرگترین عدد ذخیره میشد و در این مثال در idx اندیس (خانه) بزرگترین عدد ذخیره میشود. به همین خاطر است که در خط 15 idx را با صفر مقدار دهی کردیم که به این معنی است که فرض میکنیم که بزرگترین عدد در خانه صفرم است. ادامه کد نیز با توضیحات ارائه شده قابل فهم است
جستجو در آرایه
یکی از مسائلی که در برنامه نویسی حائز اهمیت است جستجوی یک عدد در آرایه است. جستجو در آرایه به دو صورت امکانپذیر است: ترتیبی و دودویی. در جستجوی ترتیبی همانطور که از اسمش پیداست باید عدد مورد جستجو را به ترتیب از اول تا آخر با تک تک اعداد مقایسه کرد. اما در جستجوی دودویی که در ادامه به صورت کامل توضیح داده خواهد شد سرعت جستجو به مراتب از جستجوی ترتیبی بیشتر است. این نکته نیز قابل ذکر است که جستجوی دودویی بر روی آرایه مرتب (چه به صورت صعودی مرتب و چه به صورت نزولی مرتب) صورت میگیرد و در جستجوی ترتیبی شرط مرتب بودن آرایه مهم نیست.
مثال 6 – برنامهای بنویسید که یک آرایه از ورودی دریافت کند، سپس عددی از کاربر دریافت کند و آن عدد را در آرایه جستجو کند.
#include <iostream>
int main()
{
int const n=10;
int A[n];
int i,x;
bool flag = false;
cout<<"Enter Array A:";
for(i=0; i<n ;i++)
cin>>A[i];
cout<<"Enter x";
cin>>x;
for(i=0; i<n ;i++)
if(A[i]==x){
flag=true;
break;
}
if(flag)
cout<<"exist";
else
cout<<"not exist";
return 0;
}توضیح کد:
در این برنامه هم از متغیر flag استفاده شده است. با این تفاوت که فرض را بر این گذاشتیم که عدد در آرایه وجود ندارد (بنابراین flag را برابر false قرار دادهایم) و در پیمایش خط 17 چنانچه x را پیدا کردیم flag را برابر true قرار میدهیم و از ساختار تکرار خارج میشویم.
نکته: متغیر flag از نوع bool است. بنابراین مقدار این متغیر یا true است یا false. پس در خط 23 شرط if(flag) معادل این دستور خواهد بود if(flag == true)
مثال 7 – برنامه ای بنویسید که یک آرایه مرتب از ورودی دریافت کند و سپس عدد دیگری از کاربر دریافت کند و آن عدد را در آرایه به صورت دودویی جستجو کند
در جستجوی دودویی اساسا نیمی از عناصر تنها پس از یک مقایسه حذف میشوند. برای انجام جستجو، از الگوریتم زیر استفاده میشود.
- x با عنصر میانی آرایه مقایسه میشود.
- اگر x با عنصر میانی آرایه یکی بود،یعنی x در آرایه وجود دارد.
- در غیر این صورت، اگر x بزرگتر از عنصر میانی بود، امکان دارد x در نیمه سمت راست آرایه، پس از عنصر میانی، قرار داشته باشد (شایان توجه است که همانطور که پیشتر اشاره شد، آرایه مرتب شده است. پس در این حالت، نیمهای با مقادیر بزرگتر برای ادامه جستجو گزینش میشود).
- در غیر این صورت، اگر x از عنصر میانی آرایه کوچکتر باشد، آرایه به دو نیمه شکسته شده و جستجو در نیمه سمت چپ (با مقادیر کوچکتر از میانه)، ادامه پیدا میکند.
در تصویر متحرک زیر طریقه جستجوی عدد 37 در یک آرایه مرتب به دو صورت ترتیبی و دودویی نشان داده میشود. همانطور که میبینید روش دودویی به مراتب سریعتر است.

#include <iostream>
int main()
{
int const n=10;
int A[n];
int i,x;
bool flag = false;
cout<<"Enter Array A: ";
for(i=0; i<n ;i++)
cin>>A[i];
cout<<"Enter x: ";
cin>>x;
int low = 0;
int high = n-1;
int mid;
while(low<=high){
mid = (low + high)/2;
if(x == A[mid]){
flag = true;
break;
}else if (x>A[mid])
low = mid+1;
else
high = mid - 1;
}
if(flag)
cout<<"exist";
else
cout<<"not exist";
return 0;
}در این کد برای پیدا کردن عنصر میانه نیاز به اندیس ابتدا و انتهای آرایه داریم. به همین دلیل در خط 17 و 18 low و high با اندیس صفر و n-1 مقداردهی میشود. در ساختار تکرار در هر مرحله میانگین low و high را در اندیس mid ذخیره میکنیم. (خط 22) مثلا در تصویر بالا ابتدا mid برابر 8 خواهد شد (زیرا high = 16 و low = 0 است.) در دستور if (خط 24) با یک مقایسه ساده میخواهیم بدانیم که آیا به عدد مورد نظر رسیده ایم یا نه. در مثال بالا ما به دنبال عدد 37 هستیم و عنصر mid ما برابر 23 است. از آنجایی که 37 از 23 بزرگتر است پس باید در نیمه سمت راست آرایه به دنبال عدد بگردیم. پس مقدار شرط خط 27 برابر true میشود و دستور خط 28 اجرا میشود. بنابراین مقدار low = 9 خواهد شد و همچنان high=16 خواهد بود . پس در دور بعدی تکرار mid = (16 + 9)/2 یا همان 12 خواهد شد. و این دستورات ادامه پیدا خواهد کرد.
مرتب سازی آرایه ها
یکی از مسائلی که در برنامهنویسی اهمیت زیادی دارد و الگوریتمهای زیادی برای آن نوشته شده است مساله مرتبسازی است. وجود الگوریتمهای حبابی، انتخابی، درجی، سریع ، ادغامی و چندین الگوریتم دیگر نشان از اهمیت این مساله در برنامهنویسی دارد. همه این الگوریتمها در جهت بالابردن سرعت حل مساله مرتب سازی است. در این نوشته فقط به معرفی دو الگوریتم حبابی و انتخابی پرداخته شده است.
مثال 8: برنامه ای بنویسید که یک آرایه از ورودی دریافت کند و به روش حبابی آرایه را به صورت صعودی مرتب کند.
برای توضیح این روش فرض کنید آرایه [2 1 3 4 5] را داریم و میخواهیم این آرایه را مرتب کنیم. ایده اصلی روش حبابی و انتخابی این است که در هر دو روش در هر پیمایش بزرگترین عنصر آرایه را به سمت راست آرایه شیفت میدهیم. تفاوت این دو روش در نحوه پیاده سازی این ایده است. روش حبابی را قدم به قدم روی این آرایه توضیح میدهم:
1- ابتدا، دو عنصر اول آرایه با یکدیگر مقایسه میشوند و با توجه به آنکه ۵ از 4 بزرگتر است (4<۵)، این دو عنصر با یکدیگر جا به جا میشوند:
[2 1 3 5 4] <– [2 1 3 4 5]
2- در اینجا، عناصر دوم و سوم آرایه مقایسه میشوند و با توجه به اینکه ۵ از 3 بزرگتر است (3<۵)، این دو عنصر با یکدیگر جا به جا میشوند:
[2 1 5 3 4] <– [2 1 3 5 4]
3- اکنون، عنصر سوم و چهارم آرایه مقایسه میشوند و با توجه به اینکه 1 از ۵ کوچکتر است (1<۵)، این دو عنصر با یکدیگر جا به جا میشوند:
[2 5 1 3 4] <– [2 1 5 3 4]
4- و در مرحله آخرِ پبمایش اول 5 با 2 مقایسه میشود و چون 5 از 2 بزرگتر است جای این دو عنصر با هم عوض میشود.
[5 2 1 3 4] <– [2 5 1 3 4]
تا اینجا پیمایش اول آرایه به صورت کامل انجام شد و بزرگترین عدد آرایه (که 5 است) به خانه آخر آرایه منتقل شد. در پیمایش دوم دقیقا همین الگوریتم انجام میشود با این تفاوت که دیگر نیاز نیست تا آخرین خانه آرایه حرکت کنیم (زیرا بزرگترین عدد در خانه آخر قرار گرفته است) بنابراین در پیمایش دوم تا خانه یکی مانده به آخر حرکت میکنیم. همچنین برای پیمایشهای بعدی در هر پیمایش یک واحد از بازه انتهایی پیمایش کم میشود. همه مراحل ذکر شده در تصویر متحرک زیر قابل مشاهده است:
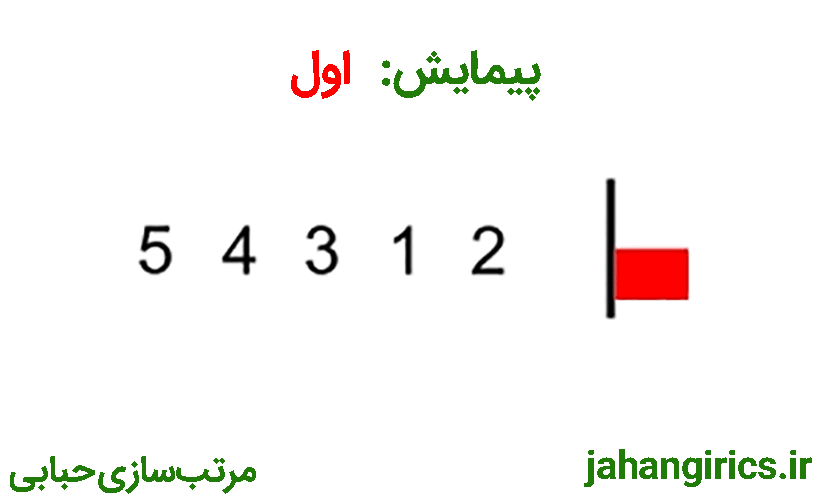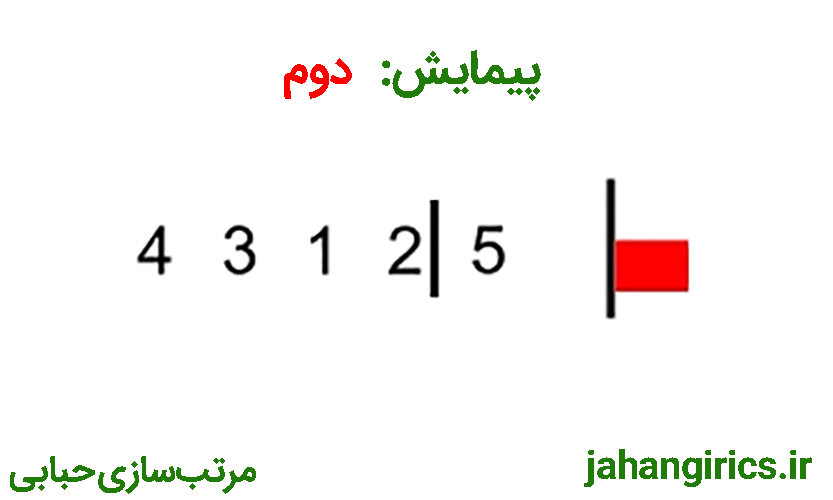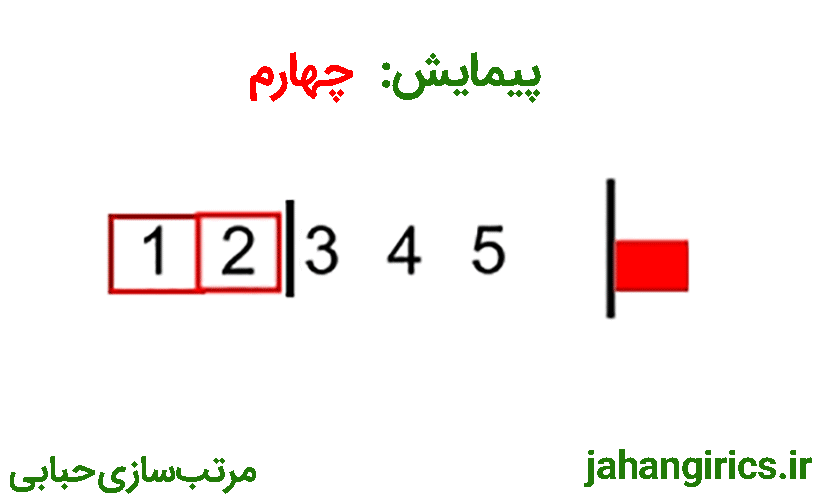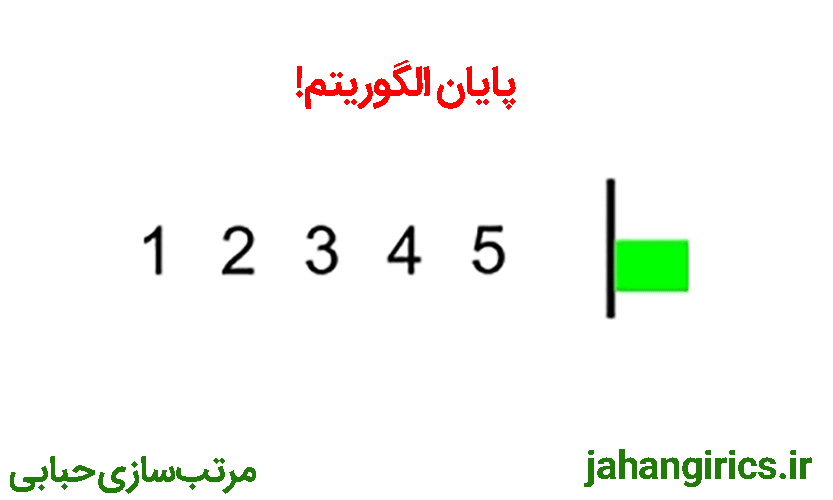
در ادامه کد این برنامه را با هم بررسی میکنیم:
#include <iostream>
#include <cmath>
int main()
{
int const n=10;
int A[n];
int i,j,temp;
cout<<"Enter Array A: ";
for(i=0; i<n ;i++)
cin>>A[i];
for(j=n-2 ; j>0;j--)
for(i=0 ; i<=j ; i++)
if(A[i] > A[i+1]){
temp = A[i];
A[i] = A[i+1];
A[i+1] = temp;
}
for(i=0; i<n ;i++)
cout<<A[i];
return 0;
}توضیح کد:
در خط 12 و 13 آرایه را از ورودی دریافت میکنیم.
قبل از توضیح ادامه کد باید به این نکته اشاره کنیم که اگر آرایه n عنصر داشته باشد (یعنی خانه های آرایه از صفر تا 1-n شماره گذاری شده باشند) در پیمایش اول باید آرایه را تا 2-n پیمایش کنیم. زیرا در هر دور تکرار باید خانه iام را با خانه بعدی یعنی خانه 1+iام مقایسه کنیم. پس حداکثر تا خانه 2-n میتوانیم حرکت کنیم زیرا به ازای مقدار i=n-2 خانه بعدی که قرار است با آن مقایسه شود 1-n خواهد شد که آخرین خانه آرایه است
در خط 15 تا 21 با حلقه for تو در تو روبرو هستیم! اول اینکه چرا به حلقه for تو در تو نیاز داریم؟ اگر یک بار دیگر بخواهیم الگوریتم را به صورت دقیقتر با هم مرور کنیم الگوریتم حبابی به این صورت است:
در پیمایش اول، آرایه از خانه صفر تا 2-n پیمایش میشود و در انتهای این پیمایش بزرگترین عدد به خانه آخر فرستاده میشود.
در پیمایش دوم، آرایه از خانه صفر تا 3-n پیمایش میشود و در انتهای این پیمایش بزرگترین عدد به خانه یکی مانده به آخر فرستاده میشود.
در پیمایش سوم، آرایه از خانه صفر تا 4-n پیمایش میشود و در انتهای این پیمایش بزرگترین عدد به خانه دو تا مانده به آخر فرستاده میشود.
.
.
.
برای پیادهسازی چنین پیمایشهایی باید از حلقه for تو در تو استفاده کرد. با هم خط 15 تا 21 را بررسی میکنیم:
در خط 15 به ازای j=n-2 وارد حلقه for میشویم در حلقه for دوم باید از i=0 تا i<=j حرکت کنیم. از آنجایی که j=n-2 است پس در حلقه for دوم i از صفر تا n-2 حرکت میکند و در هر دور تکرار خانه i را با خانه بعدی یعنی i+1 مقایسه میکند. چنانچه خانه i از i+1 بزرگتر باشد با استفاده از متغیر temp جای این دو متغیر با هم عوض میشود. وقتی حلقه for دوم تمام شد در حلقه for اول یکی از j کم میشود و j برابر n-3 میشود و اینبار به ازای j=n-3 وارد for دوم میشویم. در حلقه for دوم اینبار i از صفر تا n-3 حرکت میکند و آرایه به این صورت پیمایش میشود….
این دستورات تا زمانی که j>0 است ادامه پیدا خواهد کرد.
مثال 9: برنامه ای بنویسید که یک آرایه از ورودی دریافت کند و به روش انتخابی آرایه را به صورت صعودی مرتب کند.
در روش حبابی در هر مرحله بزرگترین عدد را به انتهای آرایه میفرستادیم و در این مثال در هر مرحله کوچکترین عدد را به ابتدای آرایه میفرستیم. توجه داشته باشید که هیچ تفاوتی بین این دو ایده نیست و صرفا برای تفاوت در پیاده سازی این دو روش این کار را انجام میدهیم. شما میتوانید روش مرتب سازی انتخابی بنویسید که در هر مرحله بزرگترین عدد را به انتهای آرایه بفرستد!
حال به پیاده سازی روش مرتب سازی انتخابی میپردازیم. همانطور که گفتیم باید در هر مرحله کوچکترین عدد آرایه را به ابتدای آرایه بفرستیم.برای اینکه بتوانیم کوچکترین عدد آرایه را به ابتدای آرایه بفرستیم نیاز است که جای کوچکترین عدد را بلد باشیم. پس از ایده idx که در بالاتر در روش جستجو توضیح دادیم باید استفاده کنیم. با یک مثال ادامه میدهیم:
آرایه [2 1 4 3 5] را در نظر بگیرید. روش انتخابی را قدم به قدم و با فرض n=5 توضیح میدهیم:
1- در پیمایش اول از خانه صفرم تا خانه چهارم حرکت میکنیم، اندیس کوچکترین عدد آرایه را پیدا میکنیم (idx=3 میشود به این معنی کوچکترین عدد در خانه سوم است که عدد یک میشود) و جای خانه صفر و 3 را باهم عوض میکنیم:
[2 5 4 3 1] <– [2 1 4 3 5]
2- در پیمایش دوم از خانه 1 تا خانه چهارم حرکت میکنیم (توجه داشته باشید کوچکترین عدد در خانه صفرم قرار گرفته و دیگر نیازی نیست در پیمایش دیده شود) اندیس کوچکترین عدد آرایه را پیدا میکنیم (که در این پیمایش idx=4 خواهد شد) و جای خانه 1 و 4 را باهم عوض میکنم:
[3 5 4 2 1] <– [2 5 4 3 1]
3- در پیمایش سوم از خانه 2 تا خانه 4 حرکت میکنیم. idx = 4 خواهد شد و جای خانه 2 و 4 با هم عوض میشود.
به همین صورت الگوریتم ادامه پیدا میکند تا آرایه مرتب شود. در تصویر متحرک زیر مطالبی که عرض شد قابل مشاهده است:

در ادامه کد مربوط به این روش را میبینید:
#include <iostream>
#include <cmath>
int main()
{
int const n=10;
int A[n];
int i,j;
cout<<"Enter Array A: ";
for(i=0; i<n ;i++)
cin>>A[i];
int idx,temp;
for(i=0;i<n;i++){
idx=i;
for(j=i+1;j<n;j++)
if(A[j]<A[idx]){
idx=j;
}
//Exchange A[idx] and A[i]
temp = A[idx];
A[idx]=A[i];
A[i]=temp;
}
for(i=0; i<n ;i++)
cout<<A[i]<<" ";
return 0;
}توضیح کد:
قسمت اصلی این کد که نیاز به توضیح دارد خط 17 تا 27 است. در حلقه for اول i از صفر تا n حرکت میکند. به ازای i=0 وارد دستورات میشود و در خط 18 idx=0 میشود به این معنی که فرض میکنیم که کوچکترین عدد در خانه صفر است. در حلقه for دوم j از یک تا آخر حرکت میکند و و با مقایسه ای که در خط 20 انجام میدهد اندیس کوچکترین عدد پیدا میشود و در خط 24 تا 26 جای A[0] و A[idx] با هم عوض میشود. بنابراین در پیمایش اول کوچکترین عدد در خانه صفر قرار میگیرد. در پیمایش بعدی i=1 میشود و به همان ترتیبی که گفت کوچکترین عنصر بعدی آرایه پیدا میشود و در خانه یک قرار میگیرد و این ترتیب ادامه پیدا میکند…
در این نوشته سعی شد مبحث آرایه ها که پیچیدگی بیشتری نسبت به آموزشهای قبلی داشت توضیح داده شود. چنانچه در فهم مثالها مشکل داشتید در قسمت نظرات سوالاتتان را بپرسید. در قسمت بعدی به سراغ آرایه دو بعدی در سی پلاس پلاس میریم:
اگه دوست دارید به آموزش کامل سی پلاس پلاس دسترسی داشته باشید میتونید از لینک زیر این دوره رو دریافت کنید:

یوتیوب پلاس سی پلاس پلاس
چرا یوتیوب پلاس ++C؟
اگر شما ویدیوهای سی پلاس پلاس من در یوتیوب رو دیده باشید از کیفیت و محتوای با ارزش ویدیوها اطلاع دارید و احتمالا به همین دلیل هم است که تصمیم گرفتید این دوره رو خریداری کنید. شما با خرید این دوره در واقع دارید کیفیت کدنویسی خودتون رو بالاتر میبرید، بعضی از تمرینهایی که برای هر جلسه در یوتیوب مشخص کردم نیاز به فکر و وقت بیشتری داره و بعضی های دیگه نیاز به جس…
 ورود / ثبت نام
ورود / ثبت نام

برنامه برای مرتب کردن اعداد تو c++میخواستم با ارایه و حلقه ترجیحا
مثال 8 و 9 همین نوشته این کار رو انجام میدن. مرتب سازی حبابی و انتخابی
میشه برنامه رو برای معکوس کردن 5 عدد هم بگین.ممنون میشم
سلام، مشابه این سوال رو در مثالهای مختلف سایت داریم ولی اگر بخواهید یک سوال جدید حل بشه به پشتیبانی سایت در تلگرام (کلیک کنید) و یا واتساپ (کلیک کنید) پیام بدید
ببخشید شما میتونید این رو حل کنید
برنامه ای بنویسید که یک آرایه ای به طول 100دریافت کنه و سپس یک عدد دیگر نیز دریافت کند و ما وقوع اولین و آخرین وقوع این عدد را تشخیص دهید؟
لطفا به تلگرام سایت پیام بدید:
@jahangiri_cs
مطالب بسیار عالی و آموزنده بود.
ممنون، خوشحالم که این مطالب برای شما مفید واقع شده.