ریاضی به چه دردی میخوره؟ انتگرال کجای زندگی به دردمون میخوره؟ مشتق بگیریم که چی بشه؟!
این نمونهای از سوالاتی است که ذهن اکثر دانشجویان را به خود مشغول کرده است. فارغ از اینکه همه ما تاحدودی با کاربرد و اهمیت انتگرال و مشتق در علوم مختلف آشنا باشیم ولی شاید کمتر از فیبوناچی شنیده باشیم. در این مقاله سعی دارم ابتدا مساله فیبوناچی را مطرح کنم و سپس در مورد تاثیرپذیری مغز انسان از این اعداد و در نهایت کاربرد ترازهای فیبوناچی در بازار سرمایه صبحت کنم.
معماي زاد و ولد خرگوش
فيبوناچي در سال 1202 به مسئله عجيبي علاقمند شد. او مي خواست بداند اگر يک جفت خرگوش نر و ماده داشته باشد و رفتاري براي زاد و ولد آنها تعريف کند در نهايت نتيجه چگونه خواهد شد. فرضيات اينگونه بود :
– شما يک جفت خرگوش نر و ماده داريد که همين الآن بدنيا آمده اند.
– خرگوشها پس از يک ماه بالغ مي شوند.
– دوران بارداري خرگوشها يک ماه است.
– هنگامي که خرگوش ماده به سن بلوغ مي رسد حتما” باردار مي شود.
– در هر بار بارداري خرگوش ماده يک خرگوش نر و يک ماده بدنيا مي آورد.
– خرگوش ها هرگز نمي ميرند.
حال سوال اينجاست که پس از گذشت يکسال چه تعداد خرگوش نر و چه تعداد خرگوش ماده خواهيم داشت؟
بد نیست قبل از اینکه ادامه مطلب را بخوانید به این سوال فکر کنید.
فرض کنیم Fn تعداد جفت خرگوش پس از n ماه باشد، میدانیم کهF1= 1 و F2=2. (زیرا در ابتدای ماه اول یک جفت خرگوش داریم و با شروع ماه دوم جفت اول جفت دوم را تولید میکند) تعداد جفت خرگوشها در ماه n+1 ام برابر خواهد بود با حاصل جمع تعداد جفت خرگوشهایی که در این ماه متولد میشوند با تعداد جفت خرگوشهای موجود(که همان Fn است) اما چون هر جفت خرگوش که از دو ماه قبل موجود بوده هماکنون حداقل دوماه سن خواهند داشت و به سن زادو ولد رسیدهاند تعداد جفت خرگوشهای متولد شده برابر خواهد بود با Fn-1 ، پس خواهیم داشت:
F1=1 , F2=2, Fn+1 = Fn + Fn-1
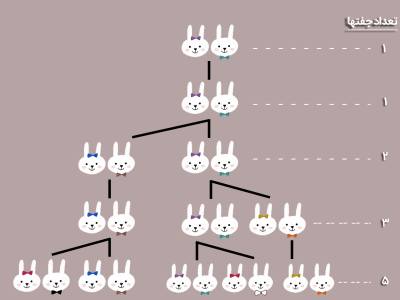
بدون اینکه به کلیت مساله خللی ایجاد شود میتوان دنباله را با 1 و 1 شروع کرد و از جمله سوم به بعد هر جمله دنباله فیبوناچی را برابر با مجموع دو جمله قبل کرد. در تصویر زیر مفاهیم ارائه شده به تصویر کشده شده است.
در ادامه به ویژگی مهم دنباله فیبوناچی میپردازیم.
دنباله فیبوناچی زیر را در نظر بگیرید:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …
نکته شگفت انگیز در این دنباله، حاصل تقسیم هر جمله از این دنباله بر جمله قبل از خود است. یعنی اگر در دنباله بالا هر جمله را بر جمله قبل از خود تقسیبم کنیم به دنباله زیر میرسیم:
1, 2, 1.5, 1.666, 1.6 , 1.625, 1.615, 1.619, 1.617, 1.618, 1.618, 1.618, …
همانطور که میبینید حاصل این تقسیم به 1.618 همگراست. اما این عدد چیست که شگفت انگیزی فیبوناچی را نشان میدهد؟ اگر این عدد را در گوگل جستجو کنید به Golden ratio یا همان عدد طلایی میرسید. بد نیست کمی از عدد طلایی صحبت کنیم.
اگر از شما این سوال پرسیده شود که هرم فراعنه و نقاشی مونالیزای داوینچی چه وجه اشتراکی با توییتر و پپسی دارند؟ تا حدی عجیب به نظر میرسد. ولی پاسخ سریع این سوال این است: همه آنها با استفاده از نسبت طلایی طراحی شدهاند. نسبت طلایی زمانی به دست میآید که یک پارهخط به دو بخش تقسیم شود و اگر بخش طولانیتر (a) را بر بخش کوتاهتر (b) تقسیم کنیم، برابر با تقسیم مجموع (b) + (a) بر (a) باشد که هر دو مقدار برابر با 1.618 هستند.
در طبیعت به وفور از نسبت طلایی استفاده شده است. شاخ و برگ درختان، دانهها آفتابگردان، بدن انسان، گردبادها و منظومهها و خیلی موارد دیگر.
جالب است بدانید که مغز انسان طوری طراحی شده است که اشیا و تصاویری را ترجیح میدهد که در آنها نسبت طلایی رعایت شده است.
این اصل مهم در طراحی ها و عکاسی ها به وفور استفاده میشود یعنی طرحها و قابهای عکاسی به گونه ای انتخاب میشوند که در آن نسبت طلایی رعایت شود.
اگر به استفاده عملی از نسبت طلایی در طراحی (لوگو، فوتوشاپ، عکاسی و …) علاقهمندید این لینک را از دست ندهید: کلیک کنید.
نسبت طلایی در بازایابی، معماری و حتی دندانپزشکی هم کاربرد دارد. درادامه کاربرد اعداد فیبوناچی در بازار سرمایه را بررسی میکنیم.

قبل از ادامه بحث کمی در مورد بازار سرمایه صحبت کنیم! اگر شما شناختی از بازار سرمایه نداشته باشید و بخواهیم بازار سرمایه را به صورت دقیق تعریف کنیم قطعا دچار سردرگمی میشوید. به طور ساده (و نه دقیق) اینگونه میتوان گفت که شما میتوانید با رصد بازار و انتخاب یک شرکت بورسی (مانند شرکت ایران خودرو، ذوب آهن، فولاد و … ) قسمتی از سرمایه خود را به خریدن سهام این شرکت اختصاص دهید. مثلا سهمی را در قیمت 100 تومان میخرید و به زمانی که قیمت به 150 تومان رسید با 50 درصد سود سهامتان را میفروشید. اما همیشه اوضاع به کام شما نیست و ممکن است قیمت سهم از 100 تومان به 80 تومان برسد و شما 20 درصد ضرر کنید. پس اینکه سهام چه شرکتی را کِی بخرید و کِی بفروشید بسیار حائز اهمیت است. اینجاست که ارزش تحلیل شما برای خرید و فروش نمایان میشود. شما میتوانید به صورت بنیادی یا تکنیکال سهام مورد بررسی خود را ارزیابی کنید و با توجه به تحلیلی که صورت میدهید اقدام به خرید یا فروش سهم کنید.
حال به دنباله فیبوناچی بازگردیم! یکی از کاربردهای مهم دنباله فیبوناچی در بورس است. شاید بتوان گفت پایه تحلیل تکنیکال در بورس دنباله فیبوناچی است. اگر به یاد داشته باشید در پست قبلی گفتیم که حاصل تقسیم هر جمله فیبوناچی بر جمله قبل از خود به عدد 1.618 همگرا میشود. در تحلیلهای بورسی تنها به تقسیم هر جمله به جمله قبل از خود توجه نمیشود، بلکه تقسیم هر جمله به جمله بعد از خود، دو جمله بعد از خود، دو جمله قبل از خود…. حائز اهمیت است. مثلا اگر بیایید هر جمله فیبوناچی را بر دو جمله قبل از خود تقسیم کنید به عدد 2.618 میرسید.
بد نیست بدانید تحلیلگران بورس اعداد 0.382، 0.618، 1.618 و 2.618 را به ترازهای فیبوناچی میشناسند و در تحلیل های خود به وفور از این اعداد استفاده میکنند. ولی چرا این اعداد در بورس مهم هستند؟ تحلیل تکنیکال بر طبق نمودار قیمت انجام می شود که حاصل عملکرد رفتار تک تک انسان ها می باشد. جمله معروف تحلیل تکنیکال می گوید : نمودار قیمت همه چیز را در خودش لحاظ می کند. از این موارد رفتار های انسانی را نیز شامل می شود.
فیبوناچی در ضمیر ناخودآگاه انسان وجود دارد و بر رفتار او بطور ناخودآگاه تاثیر می گذارد. یعنی انسان بدون آن که بداند نسبت به اعداد فیبوناچی تمایل دارد ، دنباله فیبوناتچی را زیبا می داند. این امر باعث می شود که نسبت های فیبوناتچی در معاملات افراد نیز تاثیر بگذارد. وقتی بتوانیم پیش بینی کنیم که در چه نسبت های قیمتی معامله گران واکنش خواهند داشت می توانیم از این اطلاعات برای تعیین نقاط ورود و خروج به بازار و شناسایی سطوح حمایت و مقامت استفاده کنیم. بد نیست بدانید فیبوناچی نه تنها در پیشبینی قیمت میتواند به ما کمک کند که در چرخه زمانی نیز وجود دارد. ترکیب فیبوناچی قیمتی و زمانی تحلیل دقیقتری ارائه میکند. اگر علاقهمند هستید که دانش خود را در زمینه بورس بالا ببرید مطالب آموزشی که در سایت قرار میگیرد را دنبال کنید: کلیک کنید
 ورود / ثبت نام
ورود / ثبت نام