در آموزش آرایه دو بعدی مفصل در مورد 5 پیمایش مهم آرایهها صحبت کردیم. در این نوشته که میخواهیم مثال متنوعی از آرایههای دو بعدی و ماتریسها حل کنیم قطعا به مفهوم آن پیمایش ها نیاز پیدا خواهیم کرد. پس توصیه اکید میشود که پیمایشها را بلد باشید تا مثالهای این نوشته را بهتر یاد بگیرید.
در مثالهای پیشرو درجه سختی سوالات با * مشخص شده است. ترتیب سوالات از ساده به سخت در نظر گرفته شده است.
* مثال 1- برنامه ای بنویسید که یک ماتریس 3 در 3 از ورودی دریافت کند و مجموع درایههای ماتریس را چاپ کند.
برای نوشتن این مثالها بد نیست با این نوع ادبیاتی که در ادامه توضیح داده خواهد شد به مساله نگاه کنید. برای حل این مثال شما نیاز به خواندن ماتریس دارید. قبلا این کار را کرده ایم: ماتریس را به صورت سطری پیمایش میکنیم و یکی یکی درایه های ماتریس را دریافت میکنیم. در ادامه سوال از شما خواسته شده است مجموع درایه های ماتریس را محاسبه کنید. به چه صورت امکان پذیر است؟ ماتریس را به صورت سطری پیمایش کنیم (که به تک تک درایهای ماتریس دسترسی داشته باشیم) و تک تک درایههای ماتریس را به متغیری به نام sum اضافه کنیم. همه این صحبتها را میتوان در جمله دستوری زیر خلاصه کرد:
ماتریس را به صورت سطری پیمایش کنید و اعداد را از ورودی بخوانید. سپس ماتریس را دوباره به صورت سطری پیمایش کنید و همه درایه های ماتریس را به sum اضافه کنید.
#include <iostream>
using namespace std;
int main()
{
int const m = 3, n = 3;
int A[m][n],i,j,sum;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
cin>>A[i][j];
sum=0;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
sum = sum + A[i][j];
cout<<sum;
}توضیح کد:
در خط 9 تا 11 ماتریس از ورودی دریافت شده است و در خط 13 تا 16 ماتریس پیمایش میشود و تک تک درایهها به sum اضافه میشوند.
سوال: آیا میتوانستیم در دو پیمایش بالا ماتریس را به صورت ستونی پیمایش کنیم؟
جواب: بله، در جواب مساله هیچ تفاوتی ایجاد نمیشد ولی باید دقت داشته باشید که کاربری که قرار است اعداد را وارد کند باید بداند اعداد را باید به صورت سطری وارد کند یا ستونی. مثلا ماتریس زیر را در نظر یگیرید:
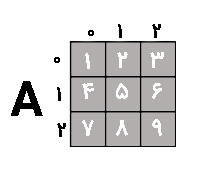
اگر شما کدی نوشته باشید که ماتریس به صورت سطری دریافت شود پس کاربر باید اعداد را به این صورت وارد کند: (از راست به چپ)
1 2 3 4 5 6 7 8 9
و چنانچه کدی نوشته باشید که ماتریس به صورت ستونی دریافت میشود پس کاربر باید اعداد را به این صورت وارد کند: (از راست به چپ)
1 4 7 2 5 8 3 6 9
در همه این مثالها از ورودی یک ماتریس 3 در 3 دریافت میشود. ولی همانطور که در کدها میبینید با تغییر مقادیر m و n به راحتی میتوانید یک ماتریس دلخواه از ورودی دریافت کنید
* مثال 2 – برنامهای بنویسید که از ورودی یک ماتریس 3 در 3 دریافت کند و بزرگترین عنصر ماتریس را چاپ کند
برای این مثال همانند مثال قبل به دو پیمایش نیاز داریم و به این صورت میتوانیم به مساله نگاه کنیم:
ماتریس را به صورت سطری پیمایش کنید و اعداد را از ورودی بخوانید. سپس درایه صفر و صفر ماتریس را در max مقداردهی اولیه کنید و ماتریس را به صورت سطری پیمایش کنید و همه درایه های ماتریس را به max مقایسه کنید. چنانچه بزرگتر باشد max را آپدیت کند.
#include <iostream>
using namespace std;
int main()
{
int const m = 3, n = 3;
int A[m][n],i,j,max;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
cin>>A[i][j];
max=A[0][0];
for(i=0;i<m;i++)
for(j=0;j<n;j++)
if(A[i][j]>max)
max = A[i][j];
cout<<max;
}توضیح کد:
همانند مثال قبل در خط 9 تا 11ماتریس از ورودی خوانده شده است. در ادامه برای پیدا کردن بزرگترین عدد ماتریس، فرض را بر این میگذاریم که A[0][0] بزرگترین عدد ماتریس است و در max ذخیره میکنیم. در خط 14 تا 17 تک تک اعداد ماتریس با max مقایسه میشوند تا بزرگترین عدد ماتریس پیدا شود.
** مثال 3- برنامهای بنویسید که یک ماتریس 3 در 3 از ورودی دریافت کند و اعدادی که از میانگین اعداد ماتریس بزرگتر است را چاپ کند.
قبل از اینکه توضیحات این مثال را بخوانید به این سوال فکر کنید که به نظر شما حل این سوال به چند پیمایش نیاز دارد؟
همیشه در مواجهه با این مسائل سعی کنید سوال بالا را پاسخ دهید. به چند پیمایش نیاز است؟ هر پیمایش چه وظیفهای دارد؟
در این مثال به 3 پیمایش نیاز است. پیمایش اول مانند همه مثالهای ماتریسی که تا کنون حل شد، پیمایشی است که ماتریس از ورودی دریافت میشود (پیمایش سطری). در پیمایش دوم مجموع اعداد محاسبه میشود که بعد از آن بتوان میانگین اعداد محاسبه شود (پیمایش سطری). و در پیمایش آخر تک تک درایه ها با میانگین محاسبه میشوند و چنانچه بزرگتر باشد در خروجی نمایش داده میشود.
نکته: همانگونه که احتمالا تا الان متوجه شدهاید منظور از پیمایش ماتریس ملاقات و دسترسی به درایههای آن پیمایش است. وقتی صحبت از پیمایش سطری است یعنی میخواهیم به صورت سطری به همه عناصر دسترسی داشته باشیم. وقتی صحبت از پیمایش قطری است یعنی میخواهیم فقط به درایهای روی قطر اصلی دسترسی داشته باشیم. (به همین صورت سایر پیمایشها رو میتوانید بررسی کنید.)
با این توضیحات کد زیر را ببینید:
#include <iostream>
using namespace std;
int main()
{
int const m = 3, n = 3;
int A[m][n],i,j,sum;
double avg;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
cin>>A[i][j];
sum = 0;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
sum = sum + A[i][j];
avg = sum /(m*n);
for(i=0;i<m;i++)
for(j=0;j<n;j++)
if(A[i][j] > avg )
cout<<A[i][j]<<" ";
}توضیح کد:
در پیمایش اول (خط 10 تا 12) ماتریس دریافت میشود.
در پیمایش دوم (خط 15 تا 17) مجموع درایههای ماتریس محاسبه و در خط 18 میانگین اعداد محاسبه میشود.
در پیمایش سوم (خط 20 تا 23) اعداد بزرگتر از میانگین چاپ میشوند.
**مثال 4 – برنامهای بنویسید که یک ماتریس از ورودی دریافت کند و تشخیص دهد که آیا ماتریس قطری است یا خیر.
ماتریسی قطری است که فقط عناصر قطر اصلی میتوانند غیر صفر باشند. با توجه به صورت سوال ممکن است این ذهننیت بوجود بیاید که به پیمایش قطری نیاز داریم. اما اگر با دقت بیشتری به مساله نگاه کنید متوجه میشوید که باید کل ماتریس را پیمایش کنیم و بررسی کنیم که آیا عناصر غیر قطر اصلی صفر هستند یا نه. برای بررسی این موضوع به متغیری به نام flag نیاز داریم. از این متغیر بارها استفاده کردهایم. این متغیر را با true مقداردهی میکنیم و فرض میکنیم ماتریس قطری است. در پیمایش سطری به دنبال نقض شدن این فرضیه میگردیم. یعنی هر جا که عنصر غیر صفر دیدم که روی قطر اصلی قرار ندارد flag را برابر false میکنیم. بنابراین به صورت خلاصه میتوان گفت برای حل این مساله به دو پیمایش سطری نیاز داریم، یکی برای خواندن ماتریس و دیگری بررسی قطری بودن ماتریس. توضیحات ارائه شده را در کد زیر میبینید:
#include <iostream>
using namespace std;
int main()
{
int const m = 3, n = 3;
int A[m][n],i,j;
bool flag = true;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
cin>>A[i][j];
for(i=0;i<m;i++)
for(j=0;j<n;j++)
if(i!=j && A[i][j]!=0)
flag =false;
if(flag == true)
cout<<"matrix ghotri ast!";
else
cout<<"matrix ghotri nist!";
}توضیح کد:
در خط 10 تا 12 آرایه A از ورودی دریافت میشود.
در خط 15 تا 18 پیمایش سطری انجام میشود و به بررسی قطری بودن ماتریس میپردازد. در خط 17 چنانچه i!=j باشد (یعنی عنصر A[i][j] روی قطر اصلی نیست) و A[i][j]!=0 باشد flag را برابر false میکنیم. (زیرا ماتریس قطری نیست.)
سوال: آیا نیاز است بعد از اینکه اولین عنصر غیر صفر (که بر روی قطر اصلی نیست) پیدا شد باز هم به بررسی بقیه عناصر ادامه دهیم؟
جواب: قطعا نه! وقتی اولین عنصر غیر صفر (که بر روی قطر اصلی نیست) پیدا شد نیازی به بررسی بقیه عناصر نداریم و با استفاده از دستور break و تغییر دادن کد به صورت زیر میتوانیم سرعت اجرای برنامه را بالاتر ببریم:
#include <iostream>
using namespace std;
int main()
{
int const m = 3, n = 3;
int A[m][n],i,j;
bool flag = true;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
cin>>A[i][j];
for(i=0;i<m && flag;i++)
for(j=0;j<n;j++)
if(i!=j && A[i][j]!=0){
flag =false;
break;
}
if(flag == true)
cout<<"matrix ghotri ast!";
else
cout<<"matrix ghotri nist!";
}کد بالا به نسبت کد قبلی در خط 15 و 19 تغییر ایجاد شده است. توجه به این نکته داشته باشید که اجرای دستور break فرمان اجرای برنامه را از حلقه for دوم خارج میکند و شرط flag که در خط 19 اضافه شده است منجر به خروج از حقله اول میشود. (زیرا وقتی که دستور break اجرا میشود مقدار flag برابر با false شده و بنابراین شرط حلقه for اول نیز false میشود.)
پیشنهاد میکنم این سوالات رو هم ببینید:
**مثال 5– برنامهای بنویسید که از ورودی یک ماتریس دریافت کند و تشخیص دهد ماتریس بالا مثلثی است یا خیر
ماتریسی بالامثلثی است که عناصر زیر قطر اصلی همگی صفر باشد. بنابراین باید ماتریس را به صورت پایین مثلثی پیمایش کنیم و بررسی کنیم که آیا همه عناصر زیر قطر اصلی صفر است یا خیر. شبیه به مساله قبل کدنویسی میکنیم:
#include <iostream>
using namespace std;
int main()
{
int const m = 3, n = 3;
int A[m][n],i,j;
bool flag = true;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
cin>>A[i][j];
for(i=0;i<m && flag;i++)
for(j=0;j<i;j++)
if(A[i][j]!=0){
flag =false;
break;
}
if(flag == true)
cout<<"matrix bala mosalasi ast!";
else
cout<<"matrix bala mosalasi nist!";
}*** مثال 6- برنامه ای بنویسید که از ورودی یک ماتریس دریافت کند و تشخیص دهد که آیا ماتریس متقارن است یا خیر.
ماتریسی متقارن است که خودش با ترانهادهاش یکسان باشد به عبارت دیگر ماتریس A متقارن است اگر و فقط اگر:

به طور مثال ماتریس 3 در 3 زیر متقارن است:

یک روش برای نوشتن کد این برنامه این است که ماتریس ترانهاده A را پیدا کنیم و بررسی کنیم که آیا A با ترانهاده اش برابر است یا نه. اما اگر به ماتریس متقارن بالا نگاه کنید متوجه یک ویژگی مهم دیگر میشوید و آن این است:
A[i][j] = A[j][i]
مثلا:
A[0][1] = A[1][0]
A[0][2] = A[2][0]
…
ما از این ویژگی استفاده میکنیم و بررسی میکنیم که آیا برای همه درایه ها A[i][j] با A[j][i] برابر است یا خیر. پس دوباره باید از متغیر flag استفاده کنیم. به این صورت که با true مقداردهی اولیه میکنیم ( و فرض میکنیم ماتریس متقارن است) و بدنبال نقض این فرضیه میگردیم. یعنی باید A[i][j] ای را پیدا کنیم که با A[j][i] برابر نباشد و flag را false کنیم. اگر چنین درایه ای پیدا نشد flag همچنان true باقی میماند و به این معنی است که ماتریس متقارن است. کد زیر را ببینید:
#include <iostream>
using namespace std;
int main()
{
int const m = 3, n = 3;
int A[m][n],i,j;
bool flag = true;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
cin>>A[i][j];
for(i=0;i<m ;i++)
for(j=0;j<n;j++)
if(A[i][j]!=A[j][i])
flag =false;
if(flag == true)
cout<<"matrix motagharen ast!";
else
cout<<"matrix motagharen nist!";
}توضیح کد:
در خط 10 تا 12 آرایه از ورودی دریافت میشود.
در خط 15 تا 18 با توضیحاتی که در بالا داده شد متقارن بودن ماتریس بررسی میشود.
سوال:
1-آیا این کد جواب درست تولید میکند؟
2-آیا این کد بهترین و سریعترین کد برای حل این مساله است؟
جواب:
1- بله
2- خیر!
در پاسخ به سوال 2 بد نیست مثال عددی بالا را یک بار دیگر بررسی کنیم. در ماتریس بالا A[0][1] = 2 است. وقتی کد بالا روی این مثال اجرا میشود به ازای i=0 و j=1 تساوی A[0][1] با A[1][0] بررسی میشود. حلقه for ادامه پیدا میکند و به ازای i=1 و j=0 دوباره این تساوی بررسی می شود. (چرا؟) پس با دقت کد بالا و توضیحی که ارائه شد متوجه میشوید که نیاز به پیمایش سطری برای بررسی متقارن بودن ماتریس نیست. کافیست که پیمایش سطری یا ستونی بر روی ماتریس داشته باشیم. در کد زیر پیمایش بالا مثلثی انجام شده است:
#include <iostream>
using namespace std;
int main()
{
int const m = 3, n = 3;
int A[m][n],i,j;
bool flag = true;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
cin>>A[i][j];
for(i=0;i<m && flag ;i++)
for(j=i+1;j<n;j++)
if(A[i][j]!=A[j][i]){
flag =false;
break;
}
if(flag == true)
cout<<"matrix motagharen ast!";
else
cout<<"matrix motagharen nist!";
}توضیح کد:
تفاوت این کد با کد قبل در نحوه پیمایش است. توجه داشته باشید که در پیمایش بالامثلثی باید j=i باشد. ولی در این کد j را از i+1 شروع کردیم. زیرا نیازی به پیماش قطر ماتریس نداریم.
***مثال 7- برنامهای بنویسید که از ورودی یک ماتریس دریافت کند و موارد زیر را نمایش دهد:
الف- حاصلجمع عناصر سطر اول ماتریس
ب- حاصلضرب عناصرستون آخر
ج – تعداد عناصر صفر ماتریس
د- کوچکترین عنصر قطر فرعی ماتریس
در قسمت الف از شما خواسته شده است حاصلجمع عناصر سطر اول ماتریس را پیدا کنید. بنابراین باید فقط سطر اول را پیمایش کنیم. با دقت به درایه های سطر اول ماتریش متوجه خواهید شد کار سختی در انتظار شما نیست:
A[0][0], A[0][1],A[0][2]
همانطور که میبینید درایه اول همه عناصر صفر است و درایه دوم از صفر تا n-1 تغییر میکند بنابراین با یک حلقه for میتوان کد این قسمت را نوشت:
for (j=0;j<n;j++)
sum = sum + A[0][j];به طریق مشابه برای قسمت ب هم همینکار را میکنم، با این تفاوت که در این قسمت حاصلضرب عناصر ستون آخر خواسته شده بنابراین با این درایه ها کار داریم:
A[0][n-1], A[1][n-1], A[2][n-1]
و کد زیر را خواهیم داشت:
for (i=0;i<m;i++)
mult= mult * A[i][n-1];
قسمت ج را با پیمایش سطری انجام میدهیم و برای قسمت د بهتر است کد نهایی برنامه را ببینید:
#include <iostream>
using namespace std;
int main()
{
int const m = 3, n = 3;
int A[m][n],i,j;
int sum, mult,counter,min;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
cin>>A[i][j];
//الف
sum=0;
for (j=0;j<n;j++)
sum = sum + A[0][j];
cout<<sum<<endl;
//ب
mult = 1;
for (i=0;i<m;i++)
mult= mult * A[i][n-1];
cout<<mult<<endl;
//ج
counter=0;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
if(A[i][j] == 0)
counter++;
cout<<counter<<endl;
//د
min = A[0][n-1];
for(i=0;i<m;i++)
if(A[i][n-i-1] < min)
min = A[i][n-i-1];
cout<<min<<endl;
}من رو در یوتیوب و اینستاگرام هم دنبال کنید:
*** مثال 8 – برنامهای بنویسید که از ورودی دو ماتریس m در n دریافت کند و مجموع دو ماتریس را چاپ کند.
اگر مثالهایی که تا اینجا حل شده است را خوب یاد گرفته باشید، نوشتن کد این مثال چندان سخت نیست. قبل از نوشتن کد الگوریتم جمع دو ماتریس را با هم بررسی میکنیم. در محاسبه جمع ماتریس A و ماتریس B باید درایه به درایه عناصر دو ماتریس را با هم جمع کنیم. مثلا C[0][0] (C ماتریس مجموع است) برابر خواهد بود با جمع A[0][0] و B[0][0]. به همین ترتیب بقیه عناصر ماتریس C را میتوان محاسبه کرد. بنابراین میتوان فرمول محاسبه C[i][j] را به این صورت نوشت:
C[i][j] = A[i][j] + B[i][j]
با توجه به این توضیحات کد زیر را میتوان نوشت:
#include <iostream>
using namespace std;
int main(){
int const m = 3, n = 3;
int A[m][n],B[m][n],C[m][n];
int i,j;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
cin>>A[i][j];
for(i=0;i<m;i++)
for(j=0;j<n;j++)
cin>>B[i][j];
for(i=0;i<m;i++)
for(j=0;j<n;j++)
C[i][j] = A[i][j]+B[i][j];
for(i=0;i<m;i++){
for(j=0;j<n;j++)
cout<<C[i][j]<<" ";
cout<<endl;
}
}توضیح کد:
در خط 10 تا 16 ماتریس A و B از کاربر دریافت میشود.
در خط 18 تا 20 ماتریس مجموع به روشی که گفته شد از ورودی دریافت میشود.
****مثال 9– برنامهای بنویسید که از ورودی دو ماتریس m*n و n*k را از دریافت و حاصلضرب دو ماتریس را حساب کند.
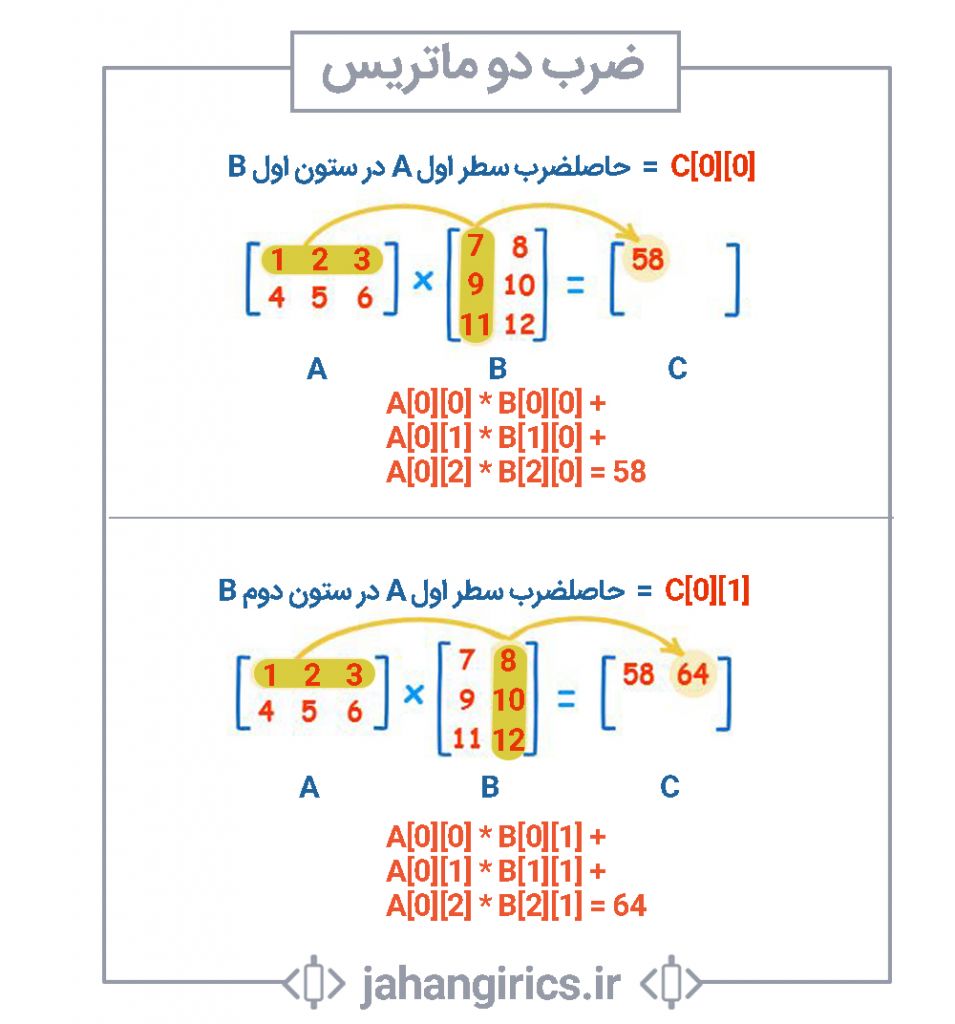
بد نیست طریقه ضرب دو ماتریس را با هم مرور کنیم. در شکل زیر قسمتی از ضرب دو ماتریس A در B نمایش داده شده است:
در شکل بالا طریقه محاسبه مقادیر C[0][0] و C[0][1] نشان داده شده است. به همین صورت C[1][0] و C[1][1] محاسبه میشود. حال برویم سراغ کد نویسی! تا اینجای کار متوجه شدید که قرار است ماتریس C ساخته شود. بنابراین نیاز است ماتریس C پیمایش شود و به ازای تک تک درایه های C محاسباتی صورت گیرد تا مقدار آن مشخص شود. پس بهتر است در مورد این موضوع صحبت کنیم:
مقدار C[i][j] چگونه محاسبه میشود؟
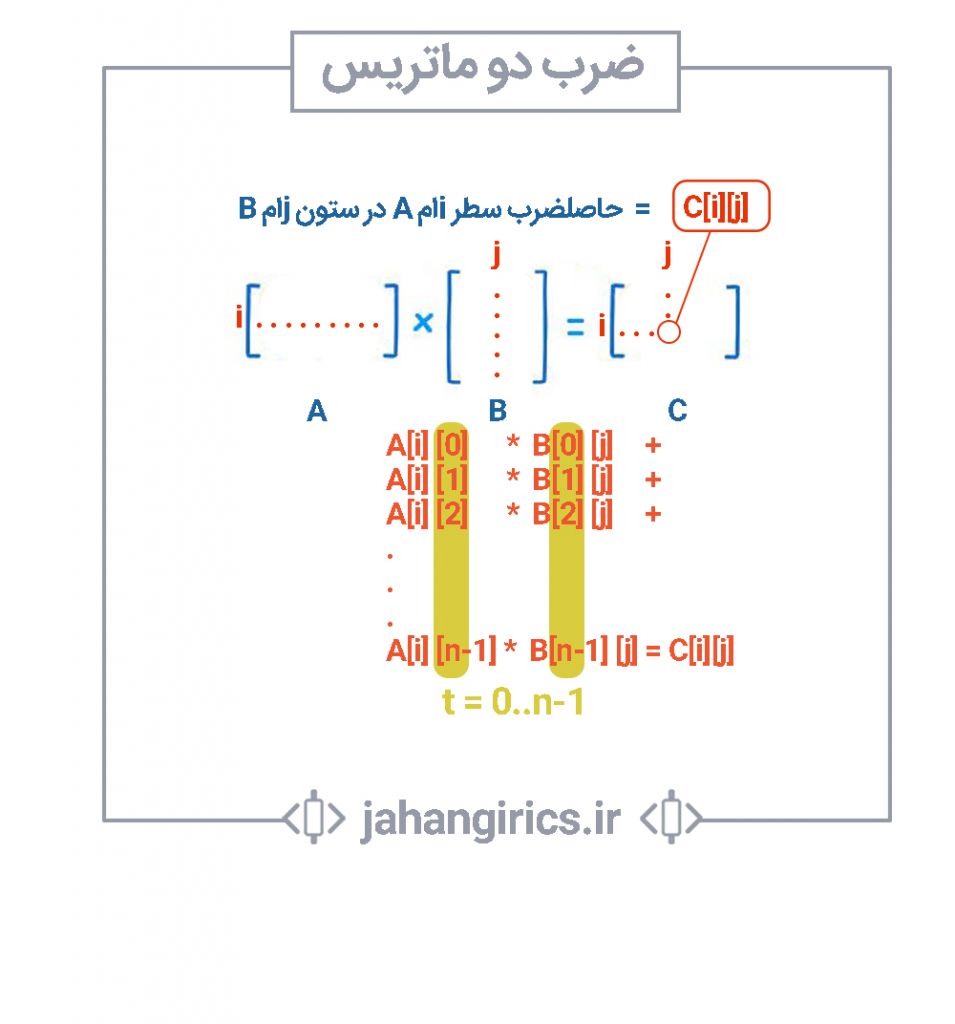
مقدار C[i][j] از حاصلضرب سطر iام ماتریس A در ستون jام ماتریس B محاسبه میشود. (اگر این جمله را متوجه نشدید بک بار دیگر به شکل بالا نگاه کنید و روند محاسبه C[0][0] و C[0][1] را مجدد بررسی کنید) پس فرمول محاسبه C[i][j] را میتوان به صورت زیر در نظر گرفت:
با توجه به توضیحات موجود در عکس نوشتن کد محاسبه C[i][j] چندان سخت به نظر نمیرسد:
C[i][j]=0; for(t=0;t<n;t++) C[i][j] = C[i][j] + A[i][t] * B[t][j];
حال که محاسبه C[i][j] را یاد گرفتیم باید این کد را در پیمایش ماتریس C قرار دهیم:
#include <iostream>
using namespace std;
int main(){
int const m = 2, n = 3, k = 2;
int A[m][n],B[n][k],C[m][k];
int i,j,t;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
cin>>A[i][j];
for(i=0;i<n;i++)
for(j=0;j<k;j++)
cin>>B[i][j];
for(i=0;i<m;i++)
for(j=0;j<k;j++){
C[i][j]=0;
for(t=0;t<n;t++)
C[i][j] = C[i][j] + A[i][t] * B[t][j];
}
for(i=0;i<m;i++){
for(j=0;j<k;j++)
cout<<C[i][j]<<" ";
cout<<endl;
}
}توضیح کد:
در خط 10 تا 16 ماتریس A و B دریافت میشود. (ماتریس m در n و ماتریس n در k)
در خط 18 تا 23 ضرب دو ماتریس محاسبه شده است. اگر به دو حلقه for خط 18 و 19 دقت کنید میبینید که در واقع ماتریس C در حال پیمایش و محاسبه شدن است و به ازای هر i و j خط 20 تا 22 (فرمولی که بالاتر توضیح داده شد) محاسبه میشود.
و در انتها، در خط 25 تا 19 ماتریس حاصلضرب C در خروجی چاپ میشود.
تا اینجا مثالهای مختلفی از ماتریسها را حل کردیم. شما با یاد گرفتن این مثالها قادر به حل طیف وسیعی از مسائل مربوط به ماتریسها خواهید بود. در اینجا نمونه ای از این مسائل را لیست میکنیم:
1- ضرب سطر اول ماتریس در یک ضریب مشخص
2- اضافه کردن سطر اول ماتریس به سطر دوم
3- جابجا کردن سطر اول و دوم ماتریس
4- جابجا کردن دو ستون دلخواه در ماتریس
جالب است بدانید در جبر خطی مساله ای تحت عنوان تجزیه LU داریم که برای نوشتن این الگوریتم به هر چهار مورد بالا نیاز است. در اینجا به هیج وجه قصد نداریم تجزیه LU را بررسی کنیم، زیرا نیاز به پیشنیازهایی از مباحث ریاضی دارد که در حوصله این نوشته نیست. با این وجود شاید بد نباشد به عنوان آخرین مثال دز این نوشته مورد سوم را با هم بررسی کنیم.
*** مثال 10- برنامه ای بنویسید که از وردی یک ماتریس دریافت کند و جای سطر اول و دوم ماتریس را با هم جابجا کند.
در مثال 7 قسمت اول پیمایش سطر اول ماتریس را توضیح دادیم. بد نیست نگاهی دوباره به کد این مساله داشته باشید. در این مساله برای پیمایش سطر اول از A[0][j] استفاده کردیم. روشن است که برای پیمایش سطر دوم به A[1][j] نیاز داریم. از آنجایی که قرار است جای سطر اول و دوم را با هم عوض کنیم باید جای A[0][j] و A[1][j] را با هم عوض کنیم. چگونه؟ با استفاده از متغیر کمکی temp:
#include <iostream>
using namespace std;
int main(){
int const m = 3, n = 3;
int A[m][n];
int i,j,temp;
for(i=0;i<m;i++)
for(j=0;j<n;j++)
cin>>A[i][j];
for(j=0;j<n;j++){
temp = A[0][j];
A[0][j] = A[1][j];
A[1][j] = temp;
}
for(i=0;i<m;i++){
for(j=0;j<n;j++)
cout<<A[i][j]<<" ";
cout<<endl;
}
}در نوشته بعدی به مثالهای کاربردی در آرایه دو بعدی خواهیم پرداخت و ذهن شما را با ساختار الگوریتمهای به کار رفته در گوگل مپ و بازی معروف candy crush آشنا میکنیم. آموزش بعدی را به هیچ وجه از دست ندهید!
اگه دوست دارید به آموزش کامل سی پلاس پلاس دسترسی داشته باشید میتونید از لینک زیر این دوره رو دریافت کنید:

یوتیوب پلاس سی پلاس پلاس
چرا یوتیوب پلاس ++C؟
اگر شما ویدیوهای سی پلاس پلاس من در یوتیوب رو دیده باشید از کیفیت و محتوای با ارزش ویدیوها اطلاع دارید و احتمالا به همین دلیل هم است که تصمیم گرفتید این دوره رو خریداری کنید. شما با خرید این دوره در واقع دارید کیفیت کدنویسی خودتون رو بالاتر میبرید، بعضی از تمرینهایی که برای هر جلسه در یوتیوب مشخص کردم نیاز به فکر و وقت بیشتری داره و بعضی های دیگه نیاز به جس…
 ورود / ثبت نام
ورود / ثبت نام

ممنون از اموزشاتون،تو مثال 7 صورت سوال حاصلضرب عناصرستون آخر خورده پایین تر تو حلش نوشتین ” حاصلضرب عناصر ستون اول ” تو حلشم ستون اولو نوشتین صورت سوالو یه تغییر ریز بدین تشکر
ممنون از دقتت، اصلاح شد 🙂
عالی ارایه هارو توضیح داده بودین
کامل و قابل فهم
ممنون