جلسه 6 – آرایه دو بعدی در سی پلاس پلاس

در آموزش آرایه در مورد مفهوم و نحوه تعریف آرایه صحبت شد. اگر با آرایه آشنایی ندارید قبل از مطالعه این قسمت، آموزش آرایه را حتما مطالعه کنید. در این آموزش در مورد آرایه دو بعدی در سی پلاس پلاس صحبت میکنیم

بعضی مواقع داده هایی که ما با آنها سر و کار داریم به فرم جدول است. مثلا:

• یک ماتریس m در n از اعداد
• جدول تناوبی
• رتبه‌بندی فیلمها توسط داوران که هر سطر نماینده نظر هر سطر و هر ستون فیلمهای متفاوت را نشان می‌دهد.
• …

با این مقدمه آموزش آرایه دو بعدی را شروع می‌کنیم:
به عناصر آرایه های دو بعدی با دو اندیس می‌توان دسترسی داشت. یکی که نماینده سطر است و دیگری که نماینده ستون. در تصویر زیر آرایه A که یک ماتریس 11 در 6 است نمایش داده شده است. همانطور که در آرایه یک بعدی دیدید اندیسها از صفر شماره‌گذاری می‌شوند.

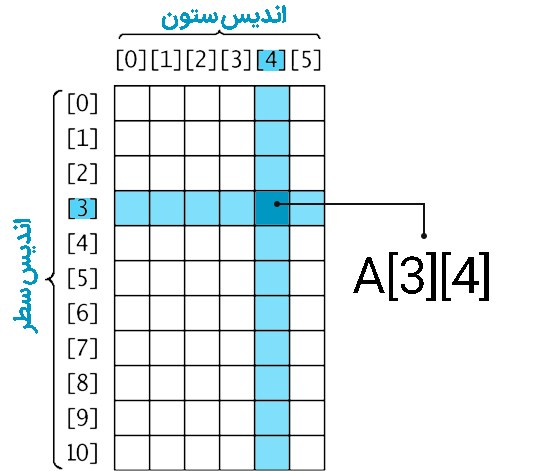
تعریف آرایه دو بعدی

آرایه دو بعدی را به صورت زیر تعریف می‌کنیم:

int const m=11, n=6;
int A[m][n];


در کد بالا آرایه دو بعدی A از جنس int تعریف شده است که m سطر و n ستون دارد. در ادامه با یک مثال ساده نحوه خواندن یک ماتریس دو بعدی را با هم یاد می‌گیریم.

مثال 1- برنامه‌ای بنویسید که از ورودی یک ماتریس 3 در 3 دریافت کند و سپس همان ماتریس را در خروجی نمایش دهد.

بهتر است کد این مثال را با ماتریس زیر توضیح دهیم:

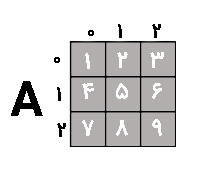
یک روش ساده و غیر هوشمندانه برای خواندن این آرایه استفاده از کد زیر است:

cin>>A[0][0];
cin>>A[0][1];
cin>>A[0][2];
cin>>A[1][0];
cin>>A[1][1];
cin>>A[1][2];
cin>>A[2][0];
cin>>A[2][1];
cin>>A[2][2];

ناگفته پیداست که این روش برای دریافت ماتریس اصلا مناسب نیست. فرض کنید بخواهید یه ماتری 10 در 10 دریافت کنید یا 100 در 100. استفاده از این روش عملا غیرممکن است. پس باید به دنبال روش هوشمندانه تری باشیم.

برای خواندن یک ماتریس به دو روش سطری و ستونی می‌توان عمل کرد. در این مثال روش سطری را توضیح می‌دهیم. روش سطری به این معنی است که باید ماتریس را سطر به سطر بخوانیم. یعنی اعدادی که از ورودی خوانده می‌شود به ترتیبی که در ماتریس بالا مشخص شده است وارد می‌شود. پس ابتدا A[0][0] خوانده می‌شود، بعد A[0][1]، بعد از آن A[0][2] (که در اینجا سطر اول خوانده شد) بعد A[1][0] و A[1][1] و … یکی یکی از ورودی دریافت می‌شود. پس ما باید کدی بنویسیم که به ترتیبی که گفته شد اعداد خوانده شود.

#include <iostream>
using namespace std;

int main()
{
	int const m=3,n=3;
	int i,j;
	int A[m][n];
	
	for (i=0;i<m;i++)
		for(j=0;j<n;j++)
			cin>>A[i][j];
			
	for (i=0;i<m;i++){
		for(j=0;j<n;j++)
			cout<<A[i][j]<<" ";		
		cout<<endl;	
	}
	
}

توضیح کد:
همانطور که در قسمت آموزش آرایه گفته شد در تعریف آرایه باید اندازه آن را به صورت ثابت و const تعریف کنیم. بنابراین در خط 6 دو متغیر m و n از نوع const تعریف شده است و در خط 8 در تعریف آرایه دوبعدی A از این دو متغیر استفاده شده است.
در خط 10 تا 12 آرایه A از ورودی دریافت شده است. نحوه دریافت آرایه از ورودی را به دقت دنبال کنید:
دو حلقه for تو در تو داریم! در حلقه اول به ازای i=0 وارد دستورات (که حلقه تکرار دوم است) می‌شویم. در حلقه دوم مقدار j از 0 تا n-1 تغییر می‌کند و در همه این تغییرات i=0 است. بنابراین به ترتیب (از چپ به راست) این خانه های آرایه از ورودی دریافت می‌شود:

A[0][0] , A[0][1] , A[0][2]

بعد از اینکه حلقه for دوم به پایان رسید یک واحد به i اضافه می‌شود و این بار یه ازای i=1 وارد حلقه for دوم می‌شویم و در این حلقه j از 0 تا n-1 تغییر می‌کند و در همه این تغییرات i=1 است. بنابراین این خانه ها دریافت می‌شود:

A[1][0] , A[1][1] , A[1][2]

و در نهایت با اضافه شدن یک واحد به i،مقدار i=2 می‌شود و این خانه ها دریافت می‌شود:

A[2][0] , A[2][1] , A[2][2]

همانطور که مشاهده می‌کنید درایه‌های این ماتریس سطر به سطر پر می‌شوند و از این رو به این پیمایش، پیماش سطری می‌گویند.

پیمایش ماتریس

وقتی که شما می‌خواهید با ماتریس کار کنید، نیاز دارید که با انواع پیمایش ماتریس آشنا باشید. این پیمایشها دید بسیار مناسبی در کدنویسی به شما می‌دهد. پس پیمایشها را با دقت دنبال کنید.

پیمایش‌هایی که مهم به نظر می‌رسند و در این آموزش به آن پرداخته شده است عبارتند از:
پیمایش سطری، پیمایش ستونی، پیمایش قطری، پیمایش بالا مثلثی و پیمایش پایین مثلثی.

1- پیمایش سطری

بالاتر این پیمایش توضیح داده شده است اما برای واضح تر شدن موضوع ماتریس زیر را نگاه کنید. اعداد قرمز رنگ ترتیب دسترسی به خانه های ماتریس را نمایش می‌دهد. پس ابتدا عدد 1 ملاقات می‌شود، سپس 2 و …
در تصاویری که در ادامه خواهید دید فرض بر آن شده است که ماتریس از ورودی دریافت شده است و می‌خواهیم کل ماتریس یا قسمتی از ماتریس را در پیمایشهای مختلف در خروجی نمایش دهیم.

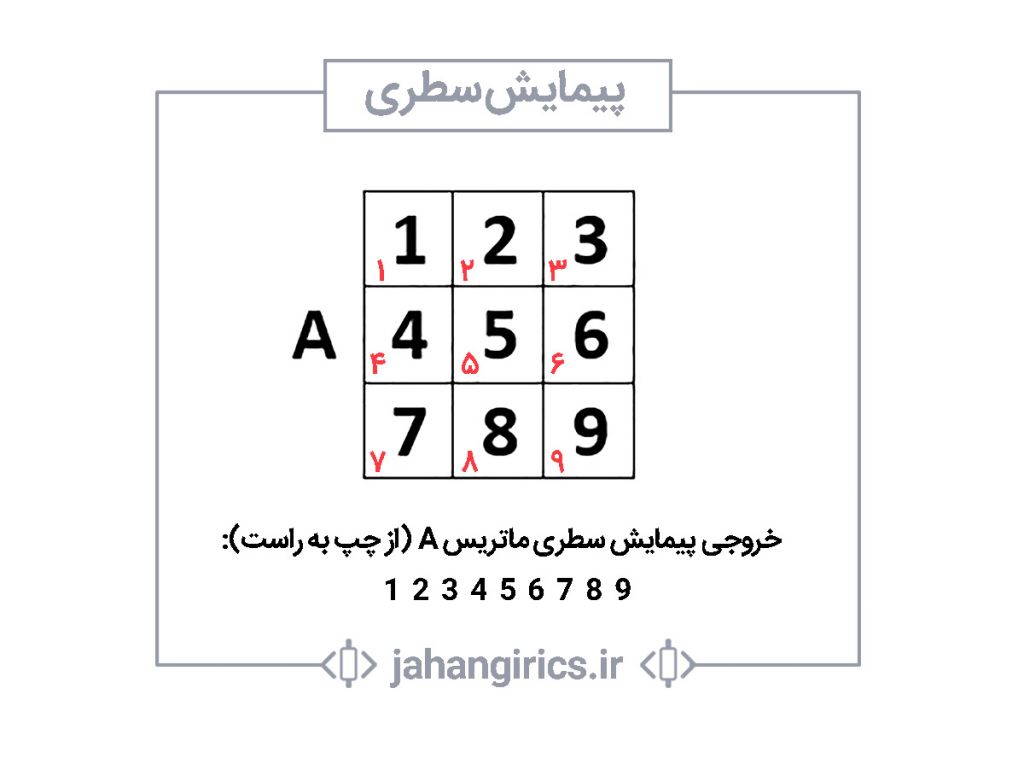
از آنجایی که کمی بالاتر در مورد پیمایش سطری توضیح داده شده است فقط به کد پیمایش سطری ماتریس A بسنده می‌کنیم:

for (i=0;i<m;i++){
	for(j=0;j<n;j++)
		cout<<A[i][j]<<" ";		

که در کد بالا m تعداد سطرهای ماتریس و n تعداد ستونها را مشخض می‌کند.

گاهی اوقات لازم است که در یک حلقه تکرار، یک یا چند حلقه دیگر هم استفاده شود. به این ساختار حلقه های تو در تو گفته می‌شود. کد بالا یک نمونه از حلقه یا for تو در تو است. اگر برای اولین بار از این ساختار استفاده می‌کنید به دقت و تمرین بیشتری برای یادگیری این ساختار دارید. در پیمایش و مثالهایی که در ادامه خواهید دید دقت و حوصله بیشتری به خرج دهید.

2- پیمایش ستونی

در پیمایش ستونی ابتدا عناصر ستون اول ملاقات می‌شوند، سپس عناصر ستون دوم و به همین ترتیب تا ستون آخر عناصر ملاقات می‌شوند. همانطور که پیش‌تر اشاره شد اعداد قرمز رنگ ترتیب ملاقات عناصر آرایه را مشخص می‌کند. بنابراین ابتدا عدد 1، سپس 4، سپس 7 و …. عناصر آرایه ملاقات می‌شود.

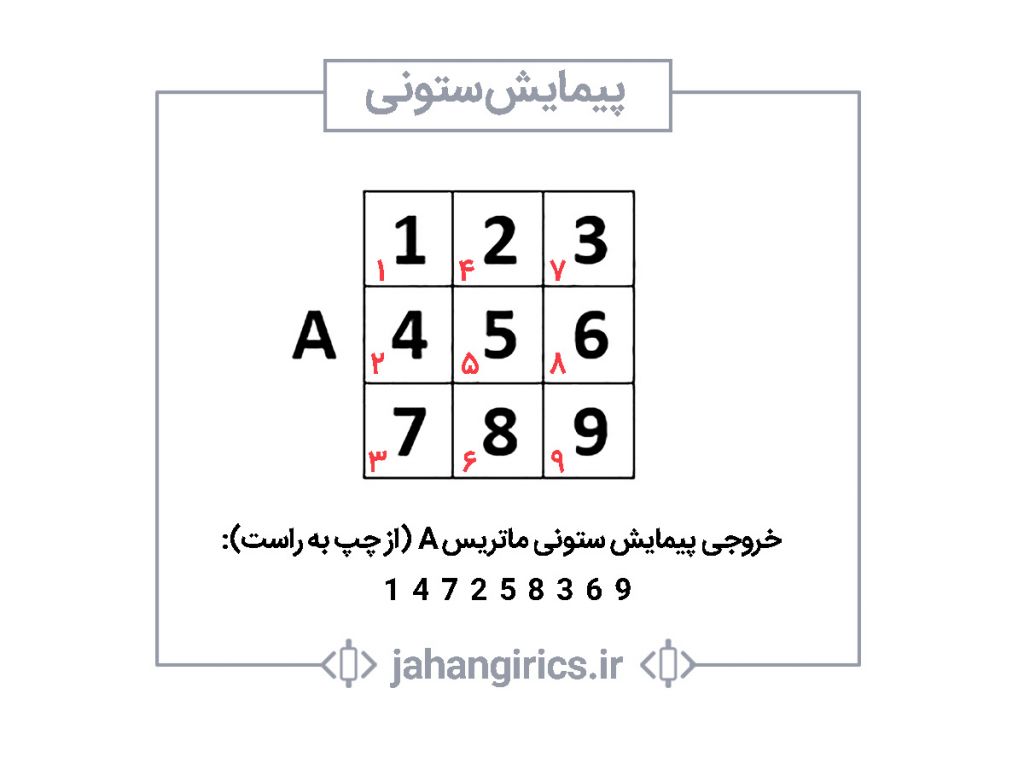
حال باید قطعه کدی بنویسیم که برای ما این پیمایش را انجام دهد. بهتر است توضیحات را بر روی کد زیر ارائه کنیم:

for(j=0;j<n;j++)
	for (i=0;i<m;i++){
		cout<<A[i][j]<<" ";		

در کد بالا ، همانند کد قبل یک حلقه for تو در تو داریم. حلقه for تو در توی بالا را با هم دنبال می‌کنیم:
در خط اول به ازای j=0 وارد حلقه تکرار می‌شویم. در بدنه این حلقه، یک حلقه تکرار دیگر تعریف شده است که در آن مقدار i از صفر تا m-1 تغییر می‌کند و در همه این تغییراتِ i، مقدار j همچنان صفر است. پس وقتی به ازای , i=0 وارد بدنه ساختار تکرار دوم می‌شویم j=0 است و در خروجی A[0][0] چاپ می‌شود. سپس یک واحد به i اضافه می‌شود و این بار در خروجی A[1][0] چاپ می‌شود و در آخرین تکرار حلقه دوم i=2 می‌شود و A[2][0] چاپ می‌شود. کار حلقه دوم که تمام شد در حلقه اول یک واحد به j اضافه می‌شود و j=1 می‌شود. بنابراین این بار به ازای j=1 وارد ساختار تکرار دوم می‌شود و در حلقه دوم مقدار i از صفر تا m-1 تغییر میکند و در همه این تغییرات مقدار j=1 است. بنابراین ابتدا A[1][0] چاپ می‌شود، سپس A[1][1] و در نهایت A[1][2]. به همین ترتیب ستون سوم نیز از ورودی دریافت می‌شود.

به صورت خلاصه اینگونه می‌توان کد را تحلیل کرد:
به ازای هر مقدار j، مقدار i از صفر تا m-1 تغییر می‌کند. بنابراین به ازای j=0 ابتدا i=0 (یعنی به A[0][0] دسترسی پیدا میکنیم) سپس i=1 (یعنی A[1][0]) و در نهایت i=2 (یعنی A[2][0]) تغییر می‌کند. در ادامه به ازای j=1، مقدار i ابتدا صفر (A[0][1]) سپس 1 و در نهایت 2 تغییر می‌کند. و در حلقه آخر به ازای j=2 مقدار i به ترتیب با 0، 1 و مقدار دهی می‌شود.

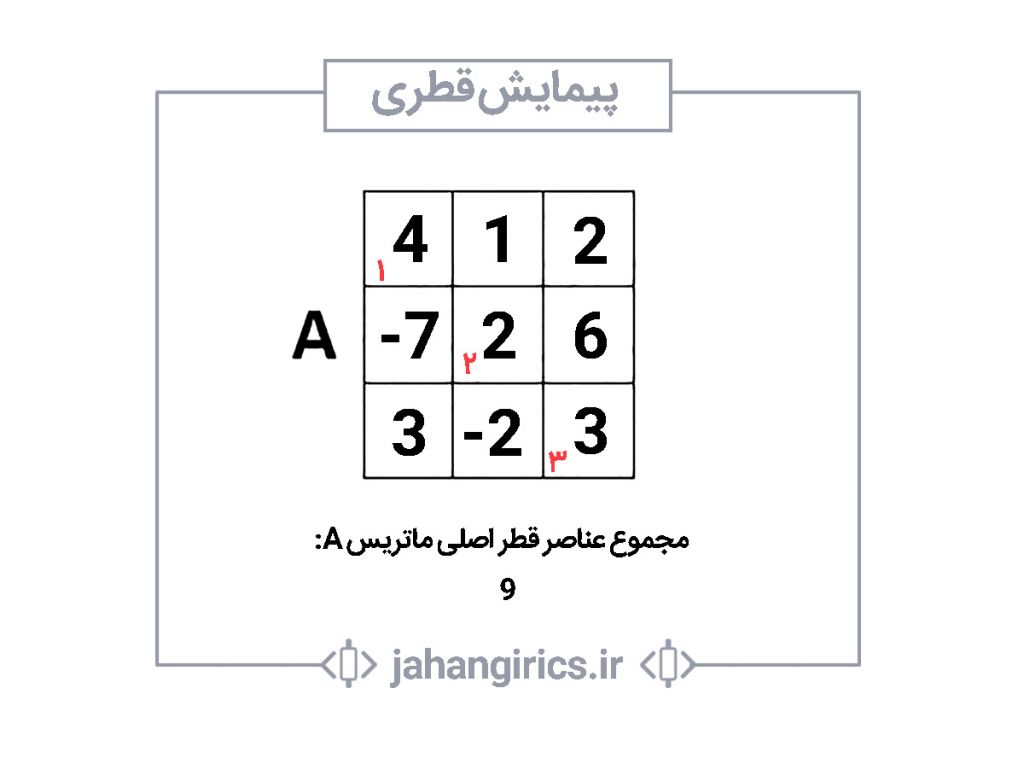
3- پیمایش قطری

این پیمایش را با یک مثال توضیح می‌دهیم.

مثال 2- برنامه ای بنویسید که یک ماتریس 3 در 3 از ورودی دریافت کند و مجموع درایه های قطر اصلی آن را چاپ کند.

همانطور که در تصویر بالا مشاهده می‌کنید باید مجموع اعداد 4، 2 , 3 در خروجی نمایش دهد. این اعداد در واقع درایه های A[0][0] و A[1][1] و A[2][2] هستند. برای این کار یک روش این است که با استفاده از پیمایش سطری (یا ستونی) همه درایه های ماتریس را ملاقات کنیم و مقدار عناصری که سطر و ستون برابر دارند را به متغیر sum اضافه کنیم. این روش به درستی جواب مساله را تولید می‌کند اما آیا این سریعترین روش است؟ قطعا خیر. در روشی که گفته شد اعداد 1، 2، 7-، 6 و -2 نیز پیمایش می‌شود، درصورتی که نیازی به این اعداد نداریم. اما اگر بتوانیم روشی پی‌ریزی کنیم که فقط اعداد روی قطر اصلی (یعنی A[0][0] و A[1][1] و A[2][2] ) پیمایش شوند قطعا روش سریعتری استفاده کرده‌ایم. بدون هیچ توضیح اضافه‌ای کد زیر را به دقت دنبال کنید و کد را تحلیل کنید:

#include <iostream>

using namespace std;

int main(){
	int const m=3,n=3;
	int i,j,A[m][n];
	
	for(i=0;i<m;i++)
		for(j=0;j<n;j++)
			cin>>A[i][j];
	
	int sum=0;
	for(i=0;i<m;i++)
		sum = sum + A[i][i];
		
	cout<<sum;			
}

توضیح کد:

در خط 9 تا 11 ماتریس A به صورت سطری از ورودی دریافت می‌شود. در خط 14 یک حلقه for تعریف شده است که در آن اندیس i از صفر تا m-1 حرکت می‌کند و در هر مرحله A[i][i] به متغیر sum اضافه می‌شود. بنابراین به ترتیب ابتدا A[0][0]، سپس A[1][1] و در نهایت A[2][2] به sum اضافه می‌شود.

حال که با این سه پیمایش آشنا شدید بهتر است به عنوان تمرین کد زیر را بر روی ماتریس مثال 2 بررسی کنید و بگویید چنانچه اعداد ماتریس مثال 2 را به عنوان ورودی به کد زیر بدهیم در خروجی چه اعداد نمایش می‌دهد.

تمرین 1: کد زیر را بر روی ماتریس مثال 2 دنبال کنید و اعدادی که این کئ در خروجی نمایش می‌دهد را به ترتیب مشخص کنید

#include <iostream>

using namespace std;

int main(){
	int const m=3,n=3;
	int i,j,A[m][n];
	
	for(i=0;i<m;i++)
		for(j=0;j<n;j++)
			cin>>A[i][j];
	
	for(i=0;i<m;i++)
		for(j=0;j<=i;j++)
			cout<<A[i][j];
		
}

در ادامه آموزش این تمرین حل خواهد شد!

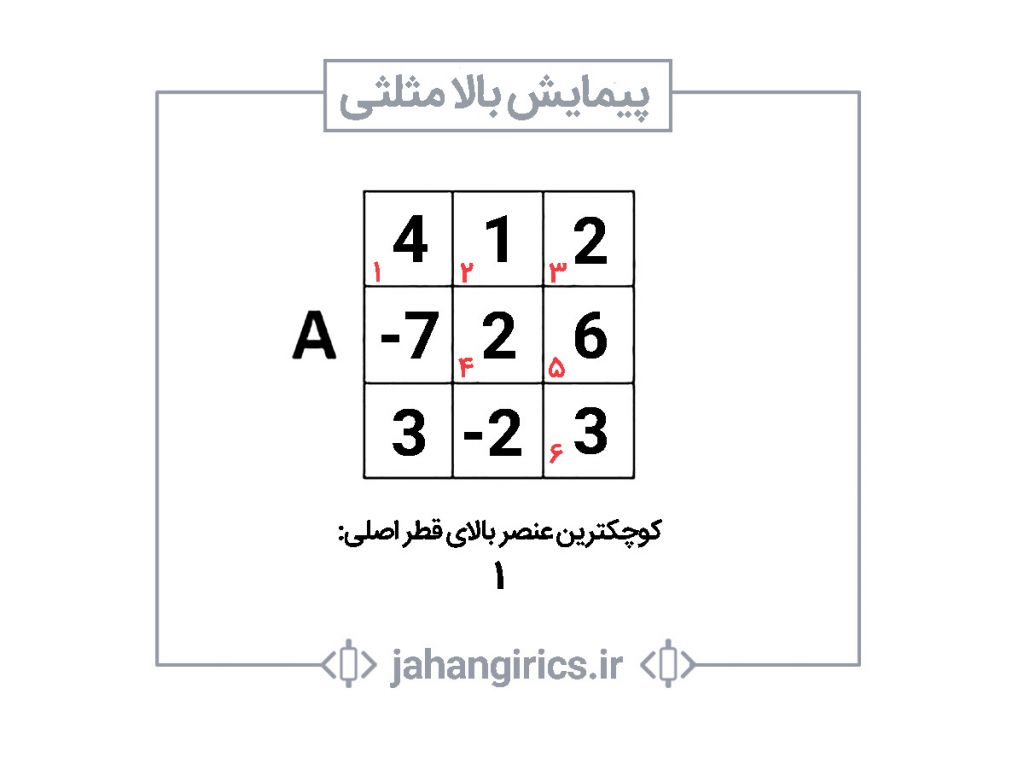
3- پیمایش بالا مثلثی

در پیمایش بالا مثلثی قطر اصلی و اعداد بالای قطر اصلی پیمایش می‌شود. بهتر است این پیمایش را در قالب مثال زیر بررسی کنیم.

مثال 3- برنامه‌ای بنویسید که از ورودی یک ماتریس 3 در 3 دریافت کند و کوچکترین عدد بالای قطر اصلی را پیدا کند.

ابتدا فرض می‌کنیم که در صورت مثال کوچکترین عنصر موجود در قطر اصلی و بالای قطر اصلی خواسته شده است.
ترتیب پیمایش درایه‌ها به همان صورتی است که با اعداد قرمز در ماتریس زیر نمایش داده شده است.

برای نوشتن کد این مثال بد نیست نکات زیر در نظر گرفته شود:
برای نوشتن پیمایش زیر همانطور که در شکل مشخص است باید همه سطرهای ماتریس پیمایش شود. پس به مانند کدهای قبل مقدار i از 0 تا m-1 تغییر می‌کند. تفاوت اصلی این پیمایش با پیمایش سطری در این است در پیمایش سطری مقدار j از 0 تا n-1 تغییر میکرد (زیرا که قرار بود همه ستونها نیز پیمایش شود ولی در پیمایش بالا مثلثی همه ستونها پیمایش نمی‍شوند. مثلا سطر دوم ماتریس را نگاه کنید (توجه کنید درایه ها در آرایه از صفر شروع می‌شود بنابراین سطر دوم در واقع آخرین سطر ماتریس است) ستون صفر و یک پیمایش نمی‌شوند و تنها ستون 2 پیمایش می‌شود. بنابراین در نوشتن حلقه j باید تغییری ایجاد شود. برای رسیدن به درک بهتر سطر به سطر نگاه کنید. در سطر صفرم ستونهای صفر تا 2 پیمایش می‌شود. در سطر یک، ستون یک تا 2 پیمایش می‌شود و در سطر دو ، ستون دو تا 2 پیمایش می‌شود. با این توضیحات ایتدا سعی کنید خودتان کد این مثال را بنویسید و سپس به کد مراجعه کنید.

#include <iostream>

using namespace std;

int main(){
	int const m=3,n=3;
	int i,j,A[m][n];
	
	for(i=0;i<m;i++)
		for(j=0;j<n;j++)
			cin>>A[i][j];
	
	
	int min = A[0][0];
	
	for(i=0;i<m;i++)
		for(j=i;j<n;j++)
			if(A[i][j] < min)
				min = A[i][j];
	
	cout<<min; 		
}

توضیح کد:
1- در خط 14 متغیر min با خانه A[0][0] مقدار دهی می‌شود. مشابه این کار را در آرایه یک بعدی با خانه A[0] انجام می‌دادیم.
2- در خط 16 تا 19 پیمایش بالامثلثی A به این صورت انجام می‌شود:
به ازای i=0 وارد ساختار تکرار می‌شویم و مقدار j از i (که همان صفر است) تا n-1 حرکت می‌کند. بنابراین همه ستونهای سطر صفرم پیمایش می‌شود.
سپس i=1 می‌شود. و در ساختار تکرار دوم مقدار j این بار از یک مقدار دهی می‌شود و تا آخر حرکت می‌کند. بنابرای در سطر یک ستونهای یک و دو پیمایش می‌شود و به همین ترتیب به ازای i=2 فقط ستون 2 پیمایش می‌شود.

نکته: در صورت سوال کوچکترین عنصر بالای قطر اصلی خواسته شده بود که ما فرض را بر این گذاشتیم که قطر اصلی هم پیمایش شود. اگر کد بالا را به خوبی متوجه شده باشید به راحتی میتوانید کد پیمایش بالای قطر اصلی را هم بنویسید. کافی است در خط 14 به جای j=i بنویسیم: j=i+1. (چرا؟)

5- پیمایش پایین مثلثی

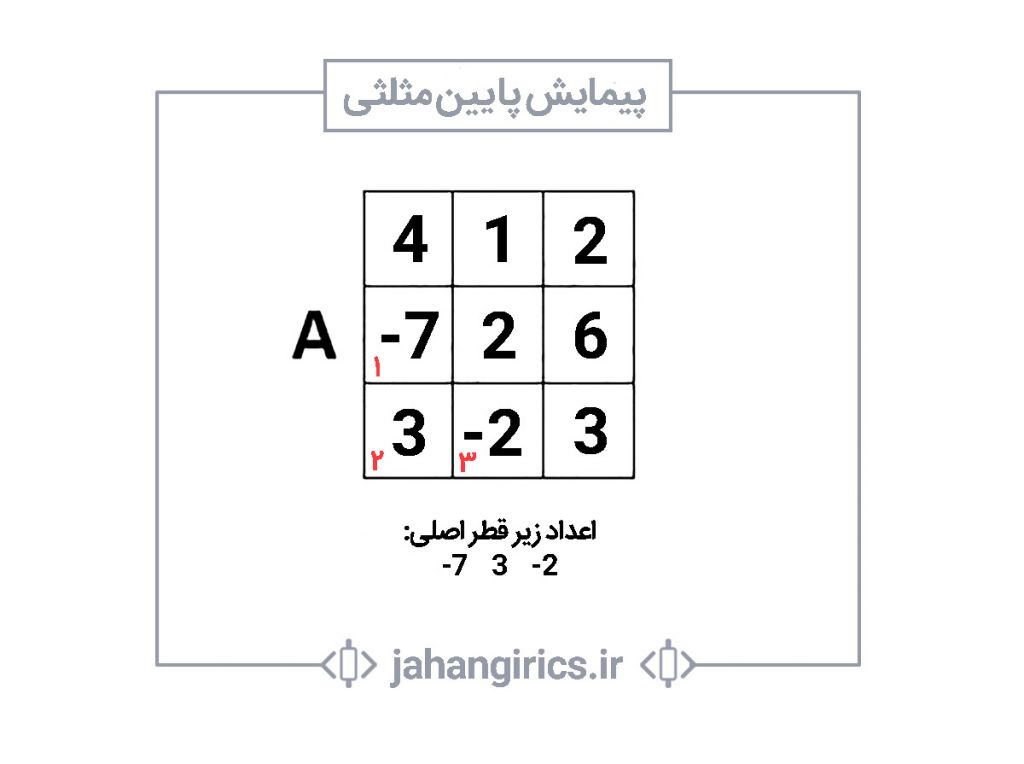
شاید تا الان متوجه شده باشید که کدی که در تمرین 1 نوشته شده است همان پیمایش پایین مثلثی است. با توجه به اینکه پیمایشهای بالا را کامل توضیح داده‌ایم نیازی به توضیح اضافه در این پیمایش نمی‌بینیم. بنابراین به مثال زیر بسنده می‌کنیم.

مثال 4: برنامه‌ای بنویسید که یک ماتریس از ورودی دریافت کند و عناصر زیر قطر اصلی را چاپ کند

#include <iostream>

using namespace std;

int main(){
	int const m=3,n=3;
	int i,j,A[m][n];
	
	for(i=0;i<m;i++)
		for(j=0;j<n;j++)
			cin>>A[i][j];
	
	
	for(i=0;i<m;i++)
		for(j=0;j<i;j++)
			cout<<A[i][j]<< " " ;
}

تا اینجا با 5 پیمایش مهم در برنامه‌نویسی آشنا شدید. نحوه پیاده‌سازی این پیمایشها فرای ماتریسهاست. به این معنی که لزوما از مفهوم این پیمایشها فقط در ماتریسها استفاده نمی‌شود. اگر مرتب‌سازی آرایه‌ها را به یاد بیاورید متوجه می‌شوید که پیمایشی که در آن مثال استفاده شد بسیار شبیه پیمایشی است که در پیمایش پایین مثلثی استفاده شد. (با این تفاوت که در مرتب سازی مقدار i از آخر به ابتدا تغییر می‌کرد و در اینجا از ابتدا به انتها)

در پست آموزشی بعدی مثالهای متنوع و زیادی در رابطه با ماتریس مطرح خواهد شد. در آن مثالها اهمیت پیمایشهایی که در این پست توضیح داده شده‌اند را متوجه خواهید شد. بنابراین توصیه می‌کنیم که 5 پیمایش ذکر شده را به دقت یاد بگیرید.

دو تا آموزش بعدی رو از دست ندید:

اگه دوست دارید به آموزش کامل سی پلاس پلاس دسترسی داشته باشید میتونید از لینک زیر این دوره رو دریافت کنید:

یوتیوب پلاس سی پلاس پلاس

چرا یوتیوب پلاس ++C؟

اگر شما ویدیوهای سی پلاس پلاس من در یوتیوب رو دیده باشید از کیفیت و محتوای با ارزش ویدیوها اطلاع دارید و احتمالا به همین دلیل هم است که تصمیم گرفتید این دوره رو خریداری کنید. شما با خرید این دوره در واقع دارید کیفیت کدنویسی خودتون رو بالاتر میبرید، بعضی از تمرینهایی که برای هر جلسه در یوتیوب مشخص کردم نیاز به فکر و وقت بیشتری داره و بعضی های دیگه نیاز…

اکنون خرید کنید